题目内容
4.探究说明:(1)如图1在△ABC中,AB=AC,点E是BC上一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G、F、D分别是垂足.求证:CD=EG+EF;
(2)如图2,在△ABC中,AB=AC,点E是BC延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC的延长线于F,CD⊥AB于D,直接猜想CD,EG,EF之间的数量关系为CD=EG-EF;
(3)如图3,边长为10的正方形ABCD的对角线相交于点O,H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG=5$\sqrt{2}$.

分析 (1)根据S△ABC=S△ABE+S△ACE,得到$\frac{1}{2}$AB•CD=$\frac{1}{2}$AB•EG+$\frac{1}{2}$AC•EF,根据等式的性质即可得到结论;
(2)由于S△ABC=S△ABE-S△ACE,于是得到$\frac{1}{2}$AB•CD=$\frac{1}{2}$AB•EG-$\frac{1}{2}$AC•EF,根据等式的性质即可得到结论;
(3)根据正方形的性质得到AB=BC=10,∠ABC=90°,AC⊥BD,根据勾股定理得到AC=10$\sqrt{2}$,由于S△BCH=S△BCE+S△BHE,得到$\frac{1}{2}$BH•OC=$\frac{1}{2}$BC•EG+$\frac{1}{2}$BH•EF,根据等式的性质即可得到结论.
解答  (1)证明:如图1,连接AE,
(1)证明:如图1,连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE+S△ACE,
∴$\frac{1}{2}$AB•CD=$\frac{1}{2}$AB•EG+$\frac{1}{2}$AC•EF,
∵AB=AC,
∴CD=EG+EF;
(2)解: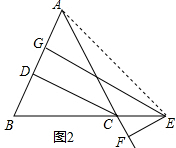 CD=EG-EF,
CD=EG-EF,
理由:连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE-S△ACE,
∴$\frac{1}{2}$AB•CD=$\frac{1}{2}$AB•EG-$\frac{1}{2}$AC•EF,
∵AB=AC,
∴CD=EG-EF;
故答案为:CD=EG-EF;
(3) 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴AB=BC=10,∠ABC=90°,AC⊥BD,
∴AC=10$\sqrt{2}$,
∴OC=$\frac{1}{2}$AC=5$\sqrt{2}$,
连接BE.
∵EF⊥BD于点F,EG⊥BC于点G,
∵S△BCH=S△BCE+S△BHE,
∴$\frac{1}{2}$BH•OC=$\frac{1}{2}$BC•EG+$\frac{1}{2}$BH•EF,
∴OC=EG+EF=5$\sqrt{2}$,
故答案为:5$\sqrt{2}$.
点评 本题考查了等腰三角形的性质,三角形面积的计算,正方形的性质,根据面积相等列方程是解题的关键.

 阅读快车系列答案
阅读快车系列答案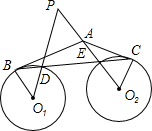 如图,AB切⊙O1于点B,AC切⊙O2于点C,BC分别交⊙O1、⊙O2于点D、E,延长O1D、O2E交于点P.若∠BAC=130°,∠ABC=20°,则∠P的度数为( )
如图,AB切⊙O1于点B,AC切⊙O2于点C,BC分别交⊙O1、⊙O2于点D、E,延长O1D、O2E交于点P.若∠BAC=130°,∠ABC=20°,则∠P的度数为( )| A. | 30° | B. | 40° | C. | 50 | D. | 60° |
| A. | 4x2-1 | B. | 2x2-1 | C. | 4x-1 | D. | 4x2+1 |
 如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(-1,n).
如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(-1,n).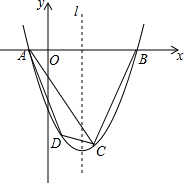 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.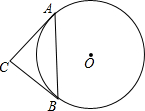 如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.
如图,已知⊙O的半径是4cm,弦AB=4$\sqrt{2}$cm,AC是⊙O的切线,切AC=4cm,连接BC.