Question

12．如图，在平面直角坐标系中，一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A（-1，n）．
（1）求反比例函数y=$\frac{k}{x}$的解析式；
（2）若P是x轴上一点，且△AOP是等腰三角形，求点P的坐标；
（3）结合图象直接写出不等式$\frac{k}{x}$+2x＞0的解集为-1＜x＜O或x＞1．

Answer 1

分析 （1）利用待定系数法即可解决．
（2）分三种情形讨论①A为顶点，②O为顶点，③P为顶点，分别求解即可．
（3）先求出两个函数图象的交点坐标，然后根据图象，反比例函数图象在上面即可解决问题．

解答 解：（1）∵点A（-1，n）在一次函数y=-2x上，
∴n=2，
∴点A坐标（-1，2）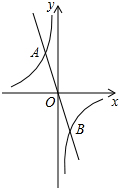
把点A（-1，2）代入y=$\frac{k}{x}$得k=-2，
∴反比例函数的解析式为y=-$\frac{2}{x}$．
（2）①当A为等腰三角形顶点时，AO=AP，此时点P坐标为（-2，0）．
②当点O为等腰三角形顶点时，OA=0P=$\sqrt{5}$，此时点P坐标为（-$\sqrt{5}$，0）或（$\sqrt{5}$，0）
③当点P为等腰三角形顶点时，OA的垂直平分线为：y=$\frac{1}{2}$x+$\frac{5}{4}$，y=0时，x=-$\frac{5}{2}$，此时点P坐标（-$\frac{5}{2}$，0）．
（3）不等式$\frac{k}{x}$+2x＞0，即$\frac{k}{x}$＞-2x，
∵一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A（-1，2），B（1.2）
∴由图象可知-1＜x＜0或x＞1．
故答案为-1＜x＜0或x＞1．

点评 本题考查反比例函数与一次函数的交点问题，灵活应用待定系数法是解决问题的关键，学会分类讨论的思想，不能漏解，属于中考常考题型．