题目内容
若P=(x-2)(x-4),Q=(x-3)2,则P与Q的关系为( )
| A、P=Q | B、P>Q |
| C、P<Q | D、P与Q的大小无法确定 |
考点:因式分解-运用公式法,非负数的性质:偶次方
专题:计算题
分析:将P与Q代入P-Q中,判断出差的正负即可得到其大小关系.
解答:解:∵P-Q=(x-2)(x-4)-(x-3)2=x2-6x+8-x2+6x-9=-1<0,
∴P<Q.
故选C
∴P<Q.
故选C
点评:此题考查了因式分解-运用公式法,以及非负数的性质,熟练掌握公式是解本题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
命题:
①对顶角相等;
②同位角相等;
③在同一平面内,垂直于同一条直线的两直线平行;
④相等的角是对顶角.
其中假命题有( )
①对顶角相等;
②同位角相等;
③在同一平面内,垂直于同一条直线的两直线平行;
④相等的角是对顶角.
其中假命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知直线y=(3m+2)x+2和y=-3x+6交于x轴上一点,则m的值为( )
| A、-2 | B、2 | C、-1 | D、0 |
为了考察某市初中3500名毕业生的数学成绩,从中抽取20本试卷,每本30份,在这个问题中,样本容量是( )
| A、3500 | B、20 |
| C、30 | D、600 |
若
有意义,则( )
| 6 |
| 3+x |
| A、x≠3 | B、x≠-3 |
| C、x<3 | D、x>3 |
点(-5,1)所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
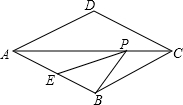 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是
如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以
如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以