题目内容
1.在等腰三角形ABC中,∠A、∠B、∠C的对边分别是a、b、c,已知a=3,b、c是关于x一元二次方程x2+mx+2-m=0的两个实数根,求△ABC的周长.分析 分两种情况讨论:①当a=b或a=c;把x=3代入方程x2+mx+2-m=0,即可得m的值 继续求即可得三角形的三边即周长②当b=c时 令△=0即可得出m的值 继续求即可得三角形三边长即周长
解答 解:①当a=b或c时,
把x=3代入x2+mx+2-m=0得m=-$\frac{11}{2}$,
方程为2x2-11x+15=0,
解得x1=3,x2=2.5;
∴a=3 b=3 c=2.5
∴三角形周长为8.5;
②当b=c时,△=0,
m2-4(2-m)=0,
解得m=2$\sqrt{3}$-2或m=-2$\sqrt{3}$-2,
方程为x2+(2$\sqrt{3}$-2)x+4-2$\sqrt{3}$=0,
解得x=1-$\sqrt{3}$,
∵1-$\sqrt{3}$<0,
∴此情况不成立,
∴三角形周长为8.5.
点评 本题考查了等腰三角形的性质,以及根的判别式、根与系数的关系,掌握三角形的三边关系定理是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
20.若x-2y的值是3,则1-2x+4y的值是( )
| A. | 7 | B. | 5 | C. | 1 | D. | -5 |
13.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{27}$=3 | D. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ |
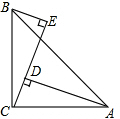 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足为D,E,那么三条线段BE、DE、AD之间的数量关系为AD-BE=DE.
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足为D,E,那么三条线段BE、DE、AD之间的数量关系为AD-BE=DE.
 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):