题目内容
4. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先根据等边三角形的性质,得到BC=AC,CD=CE,∠ACB=∠BCD=60°,然后由SAS判定△BCD≌△ACE,根据全等三角形的对应边相等即可证得①正确;又由全等三角形的对应角相等,得到∠CBD=∠CAE,根据ASA,证得△BCF≌△ACG,即可得到②正确,同理证得CF=CG,得到△CFG是等边三角形,易得③④正确.
解答 解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
∴△BCD≌△ACE(SAS),
∴AE=BD,故①正确;
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,AC=BC,
∴△BCF≌△ACG(ASA),
∴AG=BF,故②正确;
同理:△DFC≌△EGC(ASA),
∴CF=CG,
∴△CFG是等边三角形,
∴CF=CG
∴∠CFG=∠FCB=60°,
∴FG∥BE,故③④正确;
所以结论①②③④正确.
故选:D.
点评 此题考查了等边三角形的判定与性质与全等三角形的判定与性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
12.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角的度数之比为1:2:3 | B. | 三内角的度数之比为3:4:5 | ||
| C. | 三边长之比为3:4:5 | D. | 三边长的平方之比为1:2:3 |
16.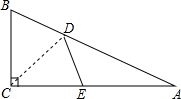 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A=23°,则∠BDC等于( )| A. | 46° | B. | 60° | C. | 68° | D. | 77° |
 如图所示是立方体的表面展开图,把它折叠成立方体,它会变成( )
如图所示是立方体的表面展开图,把它折叠成立方体,它会变成( )



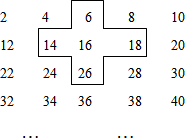 探索规律将连续的偶2,4,6,8,…,排成如表:
探索规律将连续的偶2,4,6,8,…,排成如表: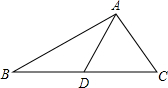 △ABC中,AD为BC边上的中线,已知AB=5,AC=3,求线段AD的长的取值范围.
△ABC中,AD为BC边上的中线,已知AB=5,AC=3,求线段AD的长的取值范围.