题目内容
19.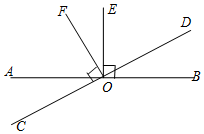 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.(1)图中∠AOF的余角是∠AOC,∠EOF,∠BOD(把符合条件的角都填出来).
(2)图中除直角相等外,还有相等的角,请写出三对:
①∠AOC=∠EOF;②∠AOF=∠EOD;③∠EOC=∠BOF.
(3)如果∠EOF=$\frac{1}{5}$∠AOD,求∠EOF的度数.
分析 (1)根据余角的定义即可得到结论;
(2)根据余角的定义,对顶角的性质即可得到结论;
(3)根据余角的定义,平角的定义即可得到结论.
解答 解:(1)∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∵∠AOC=∠BOD,
∴图中∠AOF的余角是∠AOC,∠EOF,∠BOD;
故答案为:∠AOC,∠EOF,∠BOD;
(2)①∠AOC=∠EOF,②∠AOF=∠EOD,③∠EOC=∠BOF;
故答案为:∠AOC=∠EOF,∠AOF=∠EOD,∠EOC=∠BOF;
(3)∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∴∠AOC=∠EOF,
∵∠AOC=∠BOD,
∴∠BOD=∠EOF,
∴∠AOD+∠BOD=∠AOD+∠EOF=180°,
∴∠AOD=180°-α,
∴∠AOD与∠EOF互补,
∵∠EOF=$\frac{1}{5}$∠AOD,
∴∠EOF=30°.
点评 此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线,所求角与已知角的关系转化求解.

练习册系列答案
相关题目
10. 小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
 小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )
小明在所面对的平面镜内看到他背后墙上时钟所成的像如右图所示,则此时的实际时刻应是( )| A. | 3:30 | B. | 4:30 | C. | 7:30 | D. | 8:30 |
 如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空
如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空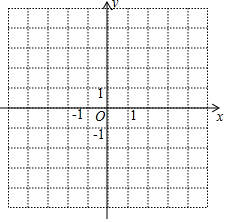 在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1).
在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1).