题目内容
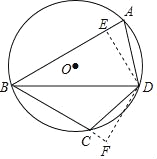
【题目】如图，矩形
中，
，
．作DE⊥AC于点E，作AF⊥BD于点F．
（1）求AF、AE的长；
（2）若以点
为圆心作圆， 
、
、
、E、F五点中至少有1个点在圆内，且至少有2个点在圆外，求
的半径 
的取值范围．
【答案】（1）
，
;（2）
【解析】
（1）先利用等面积法算出AF=
，再根据勾股定理得出;
（2）根据题意点F只能在圆内，点C、D只能在圆外，所以⊙A的半径r的取值范围为.
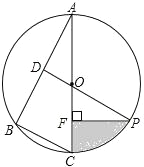
解：如图，
(1)在矩形
中，
，
．
∴DC=AB=3,AC=BD=
=5,
∵DE⊥AC，AF⊥BD，
∴
;
∴AF=，
同理，DE=,
在Rt△ADE中，AE=
=
,
(2) 若以点
为圆心作圆， 
、
、
、E、F五点中至少有1个点在圆内，则r>2.4,
当至少有2个点在圆外，r<4,
故⊙A的半径r的取值范围为：
练习册系列答案
相关题目
