题目内容
20. 如图,平行四边形ABCD的对角线相交于点O,点E在AB的延长线上,连接OE交BC于点F,若AB=6,BC=4,BE=2,求BF的长.
如图,平行四边形ABCD的对角线相交于点O,点E在AB的延长线上,连接OE交BC于点F,若AB=6,BC=4,BE=2,求BF的长.
分析 首先作辅助线:取AB的中点M,连接OM,由平行四边形的性质与三角形中位线的性质,即可求得:△EFB∽△EOM与OM的值,利用相似三角形的对应边成比例即可求得BF的值.
解答 解:取AB的中点M,连接OM,
∵四边形ABCD是平行四边形,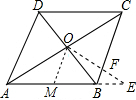
∴AD∥BC,OB=OD,
∴OM∥AD∥BC,OM=$\frac{1}{2}$AD=$\frac{1}{2}$BC=2,
∴△EFB∽△EOM,
∴$\frac{BE}{ME}$=$\frac{BF}{OM}$,
∵AB=6,AD=BC=4,BE=2,
∴ME=MB+BE=$\frac{1}{2}$AB+BE=$\frac{1}{2}$×6+2=5,
∴$\frac{2}{5}=\frac{BF}{2}$,
∴BF=$\frac{4}{5}$.
点评 此题考查了平行四边形的性质、相似三角形的判定与性质等知识.解此题的关键是准确作出辅助线,合理应用数形结合思想解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
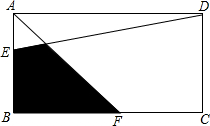 面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.
面积为1的长方形ABCD中,点E为AB的三等分点,点F为BC中点,求阴影部分的面积.