题目内容
17.用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间没有空隙,也没有重叠地铺成一片,我们称之为图形的密铺.如图,是用全等的三角形或四边形材料密铺而成的地面.
思考:
(1)用全等的正五边形材料能够密铺地面吗?
(2)用边长相同的m个正三角形和n个正方形材料组合密铺地面应满足的方程是3m+2n=12,此时m、n的值存在吗?若存在,请画出密铺地面的示意图.
(3)在边长相同的正三角形、正方形、正六边形材料中,哪几种材料组合能够密铺地面?
分析 正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解答 解:(1)∵正五边形的一个内角度数为180-360÷5=108°,不是360°的约数,∴不能密铺地面;
(2)∵∵正三角形的内角为60°,正方形的内角为90°,能组成360°,∴60°m+90°n=360,
∴满足的方程是2m+3n=12,
∵当m=3,n=2时,2m+3n=12,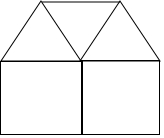
∴m、n的值存在,如图,
故答案为:2m+3n=12;
(3)∵正方形的每个内角是90°,正六边形的每个内角是120°,90m+120n=360°,m=4-$\frac{4}{3}$n,显然n取任何整数时,m不能得正整数,∴不能铺满,符合题意;
∵正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面,
∵正三角形的每个内角是60°,正六边形的每个内角是120度,∵2×60°+2×120°=360°,∴能铺满地面,
正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120度,∵60°+2×90°+120°=360°,∴能铺满地面.
∴正三角形与正方形,正三角形与正六边形,正三角形与正方形与正六边形组合能够密铺地面.
点评 本题考查平面镶嵌的知识.几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.计算:
(1)(π-3.14)0-($\frac{1}{2}$)-2+($\frac{1}{3}$)2012×(-3)2012
(2)(a2)6÷a8+(-2a)2(-$\frac{1}{2}$a2)
(1)(π-3.14)0-($\frac{1}{2}$)-2+($\frac{1}{3}$)2012×(-3)2012
(2)(a2)6÷a8+(-2a)2(-$\frac{1}{2}$a2)
2.下列命题正确的是( )
| A. | 若两弦相等,则它们所对的弧相等 | |
| B. | 若弦长等于半径,则弦所对的劣弧的度数为60° | |
| C. | 若两弧不等,则大弧所对的圆心角较大 | |
| D. | 若两弧的度数相等,则两条弧是等弧 |
 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( ) 已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.
已知:如图,AC、BD相交于点O,∠A=∠D,AB=CD.