题目内容
12. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )| A. | 8 | B. | 10 | C. | 11 | D. | 12 |
分析 作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=$\frac{1}{2}$BF=3,再利用勾股定理,可求得BH的长,继而求得答案.
解答  解:作AH⊥BC于H,作直径CF,连结BF,如图,
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴$\widehat{DE}$=$\widehat{BF}$,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=$\frac{1}{2}$BF=3.
∴BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BC=2BH=8.
故选A.
点评 此题考查了圆周角定理、垂径定理、三角形中位线的性质以及勾股定理.注意掌握辅助线的作法.

练习册系列答案
相关题目
7.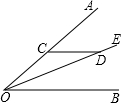 如图,OE是∠AOB的平分线,CD∥OB交OA于点C,交OE于点D,∠ACD=40°,则∠CDO的度数是( )
如图,OE是∠AOB的平分线,CD∥OB交OA于点C,交OE于点D,∠ACD=40°,则∠CDO的度数是( )
 如图,OE是∠AOB的平分线,CD∥OB交OA于点C,交OE于点D,∠ACD=40°,则∠CDO的度数是( )
如图,OE是∠AOB的平分线,CD∥OB交OA于点C,交OE于点D,∠ACD=40°,则∠CDO的度数是( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
4.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
1.下列说法中:
①有理数的绝对值一定是正数;
②互为相反数的两个数,必然一个是正数,一个是负数;
③若|a|=|b|,则a与b互为相反数;
④绝对值等于本身的数是0;
⑤任何一个数都有它的相反数.
其中正确的个数有( )
①有理数的绝对值一定是正数;
②互为相反数的两个数,必然一个是正数,一个是负数;
③若|a|=|b|,则a与b互为相反数;
④绝对值等于本身的数是0;
⑤任何一个数都有它的相反数.
其中正确的个数有( )
| A. | 0 个 | B. | 1 个 | C. | 2 个 | D. | 3 个 |
2.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
