题目内容
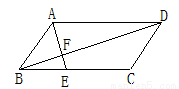
直角三角形纸片的两直角边AC与BC之比为3:4 ,将△ABC如图1那样折叠,使点C落在AB上,折痕为BD;将△ABD如图2那样折叠,使点B与点D重合,折痕为EF .则 的值为 。
的值为 。


【解析】
试题分析:直角三角形纸片的两直角边AC与BC之比为3:4,就是已知tan∠ABC= ,根据轴对称的性质,∠CBD=a,则由折叠可知∠CBD=∠EBD=∠EDB=a,∠ABC=2a,由外角定理可知∠AED=2a=∠ABC,
,根据轴对称的性质,∠CBD=a,则由折叠可知∠CBD=∠EBD=∠EDB=a,∠ABC=2a,由外角定理可知∠AED=2a=∠ABC,
∴tan∠DEA=tan∠ABC=
考点:锐角三角函数的定义;翻折变换(折叠问题)

练习册系列答案
相关题目



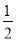 B.
B.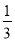 C.
C.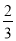 D.
D.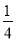
 ,则
,则 的值为
的值为 
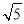 ,求DG的长.
,求DG的长.