Question

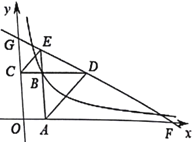
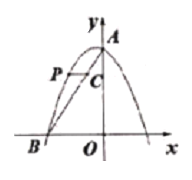
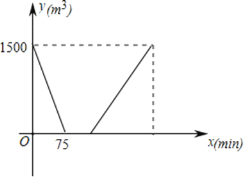
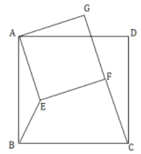
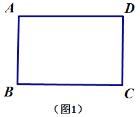
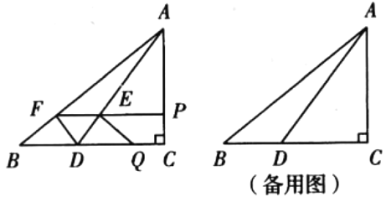
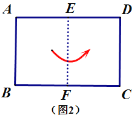
【题目】如图1，矩形纸片满足．将此矩形纸片按下列顺序折叠，则图4中的长为___________________(用含的代数式表示)．

Answer 1

【答案】

【解析】

如下图，利用折叠和矩形的特点得出△EIG是等腰直角三角形，同样得出△EJM是等腰直角三角形，然后推导出EJ的长，便可得MJ的长，从而得出MN的长．

根据题意，图形如下

∵矩形ABCD中，

∴AE=GI=BF=，∠A=90°

∵△GEI是△GEA折叠得到

∴EI=AE==GI，∠EIG=90°，

∴IF=

∴△GIE是等腰直角三角形，

∴∠IEG=45°

∵∠EFB=90°，

∴∠EJ=90°

∴△EJM是等腰直角三角形

∵IF=，

∴JI=，

∴JE=

∴在等腰直角△EJM中，JM=

∴MN=

故答案为：