题目内容
【题目】在平面直角坐标系中,已知如图所示的抛物线顶点![]() 的坐标为
的坐标为![]() ,且过点
,且过点![]() .
.
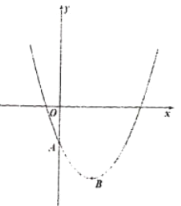
(1)求该抛物线的解析式;
(2)若点![]() 为抛物线对称轴右侧、
为抛物线对称轴右侧、![]() 轴下方一点,当
轴下方一点,当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)平移(1)中的抛物线,记平移后抛物线的顶点为![]() ,顶点
,顶点![]() 在直线
在直线![]() 上滑动,且平移后的抛物线与直线
上滑动,且平移后的抛物线与直线![]() 交于另一点
交于另一点![]() ,若点
,若点![]() 为平移前(1)中抛物线上的点,则当以
为平移前(1)中抛物线上的点,则当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)符合条件的点E的坐标为(4,-2)或(-2,4)或(
;(3)符合条件的点E的坐标为(4,-2)或(-2,4)或(![]() )或(
)或(![]() ).
).
【解析】
(1)由顶点坐标,设抛物线![]() ,然后将A点代入解析式,用待定系数法求解即可;
,然后将A点代入解析式,用待定系数法求解即可;
(2)过点B作BN⊥y轴,直线OP与抛物线对称抽BM交于点F,结合矩形的性质求得![]() ,从而得到FO=FB,设MF=x,则FO=FB=4-x,利用勾股定理求x的值,确定F点坐标,从而用待定系数法求直线解析式;
,从而得到FO=FB,设MF=x,则FO=FB=4-x,利用勾股定理求x的值,确定F点坐标,从而用待定系数法求直线解析式;
(3)线段AB的长度可求,并且在抛物线滑动过程中,线段CD的长度也是不变的,始终等于AB,因此,问题就相当于一条定长线段CD在直线AB上滑动,若![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形,则按照∠KDC=90°,KD=DC;∠KCD=90°,KC=DC;∠CKD=90°,CK=DK三种情况分析,只需利用等腰直角三角形和一次函数的图像性质求得AN的相应的距离,从而求平移后的直线解析式与原抛物线解析式相等时方程的解,可解得E点的坐标.
三点为顶点的三角形是等腰直角三角形,则按照∠KDC=90°,KD=DC;∠KCD=90°,KC=DC;∠CKD=90°,CK=DK三种情况分析,只需利用等腰直角三角形和一次函数的图像性质求得AN的相应的距离,从而求平移后的直线解析式与原抛物线解析式相等时方程的解,可解得E点的坐标.
解:(1)由题意,设抛物线![]() ,将
,将![]() 代入,得
代入,得
![]() ,解得:
,解得:![]()
∴抛物线的解析式为:![]()
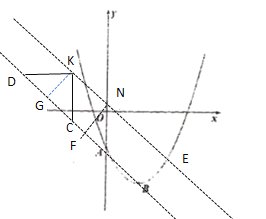
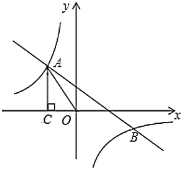
(2)如图:过点B作BN⊥y轴,直线OP与抛物线对称抽BM交于点F
由题意可知![]() ,四边形ONBM是矩形
,四边形ONBM是矩形
∴![]()
∴![]()
∴FO=FB
由B(2,-4)可得,OM=2,MB=4
设MF=x,则FO=FB=4-x
在Rt△OMF中,![]() ,解得:
,解得:![]()
∴F(2,![]() )
)
设直线OP的解析式为![]() ,把F(2,
,把F(2,![]() )代入,得
)代入,得![]()
解得:![]()
∴直线OP的解析式为![]() ;
;
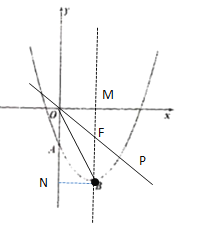
(3)∵A(0,-2),B(2,-4)
∴![]()
抛物线滑动过程中,C与B为对应点,D与A为对应点,
∴![]()
∴①当∠KDC=90°,KD=DC=![]() 时,
时,
设过点K且平行于直线AB的直线KN(直线KN与y轴交于点N)的解析式为y=-x+n
设直线AB的解析式为![]() ,则
,则![]() 解得
解得![]()
所以直线AB的解析式为:y=-x-2
∴∠FAN=45°,
∴△NFA为等腰直角三角形,则![]()
∴N(0,2)
则直线KN的解析式为y=-x+2
由此![]() ,解得
,解得![]() 或
或![]()
∴E点坐标为(4,-2)或(-2,4)
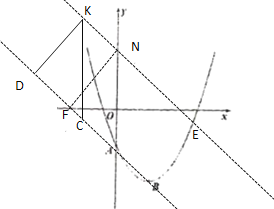
②当∠KCD=90°,KC=DC=![]() 时,同理可求,E点坐标为(4,-2)或(-2,4);
时,同理可求,E点坐标为(4,-2)或(-2,4);
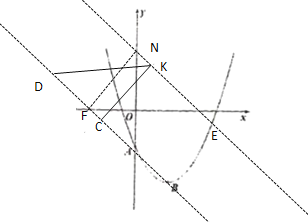
③当∠CKD=90°,CK=DK时,
过点K作KG⊥CD,此时,KG=NF=AF=![]() ,AN=2
,AN=2
∴N(0,0)
则直线KN的解析式为y=-x
由此![]() ,解得
,解得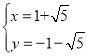 或
或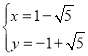
∴E点坐标为(![]() )或(
)或(![]() )
)
综上所述,符合条件的点E的坐标为(4,-2)或(-2,4)或(![]() )或(
)或(![]() ).
).