一根长为24的绳子.折成三边长为三个连续偶数的三角形.则三边长分别为6.8.10,此三角形的形状是直角三角形．题目和参考答案——青夏教育精英家教网—

题目内容

1．一根长为24的绳子，折成三边长为三个连续偶数的三角形，则三边长分别为6，8，10；此三角形的形状是直角三角形．

分析根据题意三边长为三个连续偶数，可设三边分别为：n-2，n，n+2，然后根据周长为24，列出关系式即可求出三边的长，然后由勾股定理的逆定理即可判断三角形的形状为直角三角形．

解答解：根据题意得：设三边分别为：n-2，n，n+2，
则n-2+n+n+2=24，
解得：n=8，
所以n-2=6，n+2=10，
所以三边长分别为：6，8，10；
∵6²+8²=10²，
∴此三角形的形状是直角三角形．
故答案为：6，8，10；直角三角形．

点评此题主要考查了勾股定理的逆定理，一元一次方程的应用，解题的关键是先求出三边长．

练习册系列答案

相关题目

11．

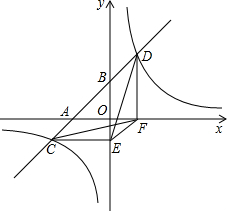如图，一次函数y=ax+b的图象与x轴，y轴交于A，B两点，与反比例函数y=$\frac{k}{x}$的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：
①S_△CEF=S_△DEF；②△AOB相似于△FOE；③△DCE≌△CDF；④AC=BD
其中正确的结论是①②④．（把你认为正确结论的序号都填上）

12．计算：$\sqrt{27}-3\sqrt{2}×（\sqrt{6}-\sqrt{\frac{2}{3}}）$．

9．若$\sqrt{{{（b-3）}^2}}=3-b$，则b的取值范围是（　　）

16．今年国庆节期间，峨眉山共接待游客约63.9万人次，较去年同期增长32.15%．63.9万用科学记数法表示为（　　）

6．已知α，β为整数，有如下两个代数式2^2α，$\frac{2}{4^β}$
（1）当α=-1，β=0时，求各个代数式的值；
（2）问它们能否相等？若能，则给出一组相应的α，β的值；若不能，则说明理由．

13．

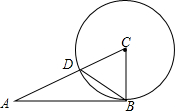已知△ABC，以顶点C为圆心、CB为半径作圆交AC于点D，连接DB．若∠ACB=2∠ABD，
①求证：边AB所在直线于⊙C相切；
②AC=3，BC=2，求AD和DB的长．

10．①分解因式：（x+2）（x-6）+16
②用简便方法计算：899×901+1．

11．数据0，1，1，3，3，4的中位数和平均数分别是（　　）

试题分类