题目内容
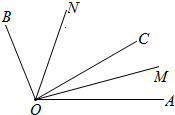 如图,射线OC在∠AOB的内部,射线OM是∠AOC的平分线,射线ON是∠BOC的平分线.
如图,射线OC在∠AOB的内部,射线OM是∠AOC的平分线,射线ON是∠BOC的平分线.(1)若∠AOM=15°,∠NOM=4∠COM,求∠AOB的度数;
(2)在(1)的条件下,射线OD在∠BOC的内部,当射线OC是∠AOD的一条三等平分线时,请在备用图中画出射线OD,再求∠DON的度数.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据题意得出∠NOM=4∠COM=60°,从而得出∠AOB的度数;
(2)先画图,可得出∠AOD=45°,即可得出∠BOD=75°,再根据∠BON=45°,再计算得出∠DON的度数.
(2)先画图,可得出∠AOD=45°,即可得出∠BOD=75°,再根据∠BON=45°,再计算得出∠DON的度数.
解答: 解:(1)∵射线OM是∠AOC的平分线,射线ON是∠BOC的平分线,
解:(1)∵射线OM是∠AOC的平分线,射线ON是∠BOC的平分线,
∴∠BON=∠CON=
∠BOC,∠AOM=∠COM=
∠AOC,
∵∠AOM=15°,∠NOM=4∠COM,
∴∠MON=60°,
∴∠CON=45°,
∴∠AOB=120°;
(2)如图,∵射线OC是∠AOD的一条三等平分线,
∴∠COD=15°,
∴∠AOD=45°,
∴∠BOD=75°,
∵∠BON=45°,
∴∠DON=∠BOD-∠BON=75°-45°=30°.
 解:(1)∵射线OM是∠AOC的平分线,射线ON是∠BOC的平分线,
解:(1)∵射线OM是∠AOC的平分线,射线ON是∠BOC的平分线,∴∠BON=∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOM=15°,∠NOM=4∠COM,
∴∠MON=60°,
∴∠CON=45°,
∴∠AOB=120°;
(2)如图,∵射线OC是∠AOD的一条三等平分线,
∴∠COD=15°,
∴∠AOD=45°,
∴∠BOD=75°,
∵∠BON=45°,
∴∠DON=∠BOD-∠BON=75°-45°=30°.
点评:本题考查了角的计算,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将直线y=-2x+3向下平移2个单位所得的直线解析式是( )
| A、y=-2x+7 |
| B、y=-2x+5 |
| C、y=-2x-1 |
| D、y=-2x+1 |
 已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长.
已知:如图,在△ABC中,∠ABC和∠ACB的平分线交于点D.过点D作EF∥BC交AB于点E,交AC于点F,若BE+CF=9cm,求线段EF的长. 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下: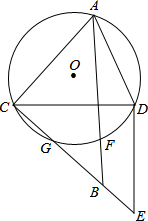 已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.
已知⊙O为△ACD的外接圆,过C作CE⊥AC,交⊙O于G,联结ED,∠CDE=90°,点B为CE上一点,使得CA=CB=CD,⊙O交AB于点F.求证:F为△CDE的内心.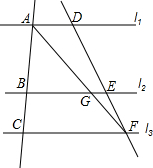 如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长. 如图,角的顶点是
如图,角的顶点是