题目内容
16. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=$\frac{4}{3}$,反比例函数y=$\frac{k}{x}$的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于-24.
如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=$\frac{4}{3}$,反比例函数y=$\frac{k}{x}$的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于-24.
分析 易证S菱形ABCO=2S△CDO,再根据tan∠AOC的值即可求得菱形的边长,即可求得点C的坐标,代入反比例函数即可解题.
解答 解:作DE∥AO,CF⊥AO,设CF=4x,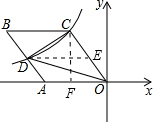
∵四边形OABC为菱形,
∴AB∥CO,AO∥BC,
∵DE∥AO,
∴S△ADO=S△DEO,
同理S△BCD=S△CDE,
∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE,
∴S菱形ABCO=2(S△DEO+S△CDE)=2S△CDO=40,
∵tan∠AOC=$\frac{4}{3}$,
∴OF=3x,
∴OC=$\sqrt{{OF}^{2}{+CF}^{2}}$=5x,
∴OA=OC=5x,
∵S菱形ABCO=AO•CF=20x2,解得:x=$\sqrt{2}$,
∴OF=$3\sqrt{2}$,CF=$4\sqrt{2}$,
∴点C坐标为(-$3\sqrt{2}$,$4\sqrt{2}$),
∵反比例函数y=$\frac{k}{x}$的图象经过点C,
∴代入点C得:k=-24,
故答案为-24.
点评 本题考查了菱形的性质,考查了菱形面积的计算,本题中求得S菱形ABCO=2S△CDO是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.10名初中毕业生的中招体育加试成绩(单位:分)统计如表:
则这组数据的平均数和中位数分别为( )
| 成绩/分 | 66 | 67 | 68 | 69 | 70 |
| 人数 | 1 | 4 | 1 | 2 | 2 |
| A. | 67,67.5 | B. | 68,68 | C. | 68,67.5 | D. | 67.5,68 |
7.方程$\frac{2}{x+3}$=$\frac{1}{x-1}$的解为( )
| A. | x=3 | B. | x=4 | C. | x=5 | D. | x=-5 |
8.一元二次方程3x2-1=2x+5两实根的和与积分别是( )
| A. | $\frac{3}{2}$,-2 | B. | $\frac{2}{3}$,-2 | C. | $-\frac{2}{3}$,2 | D. | $-\frac{3}{2}$,2 |
5.如图是一个几何体的三视图,则这个几何体是( )


| A. | 三棱柱 | B. | 圆柱 | C. | 圆台 | D. | 圆锥 |
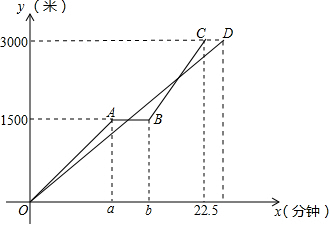 “低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题: