题目内容
4.威丽商场销售A,B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元;
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件.如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
分析 (1)设A种商品售出后所得利润为x元,B种商品售出后所得利润为y元.由售出1件A种商品和4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1100元建立两个方程,构成方程组求出其解就可以;
(2)设购进A种商品a件,则购进B种商品(34-a)件.根据获得的利润不低于4000元,建立不等式求出其解就可以了.
解答 解:(1)设每件A种商品售出后所得利润为x元,每件B种商品售出后所得利润为y元.由题意,得
$\left\{\begin{array}{l}{x+4y=600}\\{3x+5y=1100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=200}\\{y=100}\end{array}\right.$
答:每件A种商品售出后所得利润为200元,每件B种商品售出后所得利润为100元.
(2)设购进A种商品a件,则购进B种商品(34-a)件.由题意,得
200a+100(34-a)≥4000,
解得:a≥6
答:威丽商场至少需购进6件A种商品.
点评 本题考查了列二元一次方程组解实际问题的运用及二元一次方程组的解法,列一元一次不等式解实际问题的运用及解法,在解答过程中寻找能够反映整个题意的等量关系是解答本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
15.已知关于x的分式方程$\frac{3x-a}{x-3}$=$\frac{1}{3}$的解是非负数,那么a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a≥1且a≠9 | D. | a≤1 |
9.若关于x的方程kx2-3x-$\frac{9}{4}$=0有实数根,则实数k的取值范围是( )
| A. | k=0 | B. | k≥-1且k≠0 | C. | k≥-1 | D. | k>-1 |
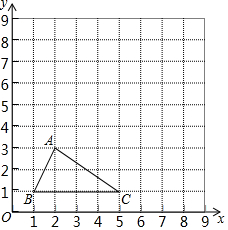 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).
在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1). 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=$\frac{4}{3}$,反比例函数y=$\frac{k}{x}$的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于-24.
如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=$\frac{4}{3}$,反比例函数y=$\frac{k}{x}$的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于-24.