题目内容
8.如果向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow x$满足$\overrightarrow x$+$\overrightarrow a$=$\frac{3}{2}$($\overrightarrow a$-$\frac{2}{3}$$\overrightarrow b$),那么$\overrightarrow x$用$\overrightarrow a$、$\overrightarrow b$表示正确的是( )| A. | $\overrightarrow a-2\overrightarrow b$ | B. | $\frac{5}{2}\overrightarrow a-\overrightarrow b$ | C. | $\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
分析 利用一元一次方程的求解方法,求解此题即可求得答案.
解答 解:∵$\overrightarrow x$+$\overrightarrow a$=$\frac{3}{2}$($\overrightarrow a$-$\frac{2}{3}$$\overrightarrow b$),
∴2($\overrightarrow x$+$\overrightarrow a$)=3($\overrightarrow a$-$\frac{2}{3}$$\overrightarrow b$),
∴2$\overrightarrow x$+2$\overrightarrow a$=3$\overrightarrow a$-2$\overrightarrow b$,
∴2$\overrightarrow x$=$\overrightarrow a$-2$\overrightarrow b$,
解得:$\overrightarrow x$=$\frac{1}{2}$$\overrightarrow a$-$\overrightarrow b$.
故选D.
点评 此题考查了平面向量的知识.此题难度不大,注意掌握一元一次方程的求解方法是解此题的关键.

练习册系列答案
相关题目
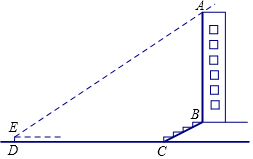 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) 如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;
如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3; 已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=$\frac{2}{3}$
已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=$\frac{2}{3}$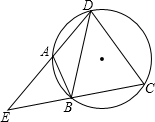 如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)
如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)