题目内容
9.已知G是等腰直角△ABC的重心,若AC=BC=2,则线段CG的长为$\frac{2}{3}\sqrt{2}$.分析 根据三角形的重心到顶点的距离等于到对边中点的距离的2倍解答即可.
解答 解:∵G是等腰直角△ABC的重心,AC=BC=2,
∴CG=$\frac{2}{3}×\frac{2}{\sqrt{2}}=\frac{2}{3}\sqrt{2}$,
故答案为:$\frac{2}{3}\sqrt{2}$
点评 本题考查了三角形的重心,熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键.

练习册系列答案
相关题目
4.已知一个坡的坡比为i,坡角为α,则下列等式成立的是( )
| A. | i=sinα | B. | i=cosα | C. | i=tanα | D. | i=cotα |
19.数轴上到原点的距离是$\sqrt{3}$的点表示的数是( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;
如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3; 已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=$\frac{2}{3}$
已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=$\frac{2}{3}$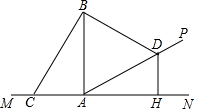 如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=7米,AD=12米,坡角为30°,试求电线杆AB的高度;(精确到0.1米)
如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=7米,AD=12米,坡角为30°,试求电线杆AB的高度;(精确到0.1米)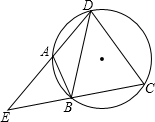 如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)
如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)