题目内容
20.已知:实数a、b、c满足方程组$\left\{\begin{array}{l}{a+b=8}\\{ab-{c}^{2}+8\sqrt{2}c=48}\end{array}\right.$,求a+b-c的值.分析 把a+b=8化为b=8-a后代入第二个方程,根据完全平方公式进行变形,再根据非负数的性质求出a、c的值,代入计算即可得到答案.
解答 解:$\left\{\begin{array}{l}{a+b=8①}\\{ab-{c}^{2}+8\sqrt{2}c=48②}\end{array}\right.$,
由①得,b=8-a③,
把③代入②得,(a-4)2+(c-4$\sqrt{2}$)2=0,
即a-4=0,c-4$\sqrt{2}$=0,
解得a=4,c=4$\sqrt{2}$,
a+b-c=8-4$\sqrt{2}$,
故答案为:8-4$\sqrt{2}$.
点评 本题考查的是高次方程的解法和完全平方公式的应用,正确运用代入法解方程是解题的关键,注意非负数的性质的应用,几个非负数的和为0,那么每一个非负数都为0.

练习册系列答案
相关题目
10.下列命题中,是假命题的是( )
| A. | 平行四边形的两组对边分别相等 | |
| B. | 两组对边分别相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是矩形 |
5.二次函数y=x2+4x-5的图象的对称轴为( )
| A. | x=4 | B. | x=-4 | C. | x=2 | D. | x=-2 |
13.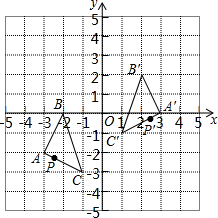 如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
 如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )| A. | (-a,b-2) | B. | (-a,b+2) | C. | (-a+2,-b) | D. | (-a+2,b+2) |
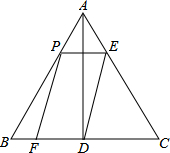 如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED,以PE、ED为邻边作?PEDF.设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连结ED,以PE、ED为邻边作?PEDF.设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
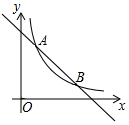 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.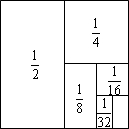 如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.
如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形,接着把一个面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$的矩形…如此进行下去.