题目内容
15.BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD=$\sqrt{3}$,则CD的长为2$+\sqrt{3}$或2-$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.分析 分两种情况:①如图1,∠A为钝角,AB=AC,在Rt△ABD中,根据锐角三角函数的定义即可得到结果;②如图2,∠A为锐角,AB=AC,在Rt△ABD中根据锐角三角函数的定义即可得到结果;③如图3,∠A为底角,由tan∠ABD=$\sqrt{3}$,得到∠ABD=60°于是得到∠A=30°,求得∠C=120°,在Rt△BCD中根据锐角三角函数的定义即可得到结果.
解答 解:分三种情况:
①如图1,∠A为钝角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=$\sqrt{3}$,
∴AD=$\sqrt{3}$,AB=2,
∴AC=2,
∴CD=2+$\sqrt{3}$,
②如图2,∠A为锐角,AB=AC,
在Rt△ABD中,∵BD=1,tan∠ABD=$\sqrt{3}$,
∴AD=$\sqrt{3}$,AB=2,
∴AC=2,
∴CD=2-$\sqrt{3}$,
③如图3,∠A为底角,
∵tan∠ABD=$\sqrt{3}$,
∴∠ABD=60°,
∴∠A=30°,
∴∠C=120°,
∴∠BCD=60°
∵BD=1,
∴CD=$\frac{\sqrt{3}}{3}$;
④∠C为锐角且为顶角时,
如图4,∵BD⊥AC,
∴∠ADB=90°,
∵tan∠ABD=$\sqrt{3}$,
∴∠ABD=60°,
∴∠A=30°,
∵∠CBA=∠A=30°,∴∠C=120°>90°,
∴这种情况不存在;
综上所述;CD的长为:2$+\sqrt{3}$或2-$\sqrt{3}$或$\frac{\sqrt{3}}{3}$,
故答案为:2$+\sqrt{3}$或2-$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
点评 本题考查了等腰三角形的性质,解直角三角形,难点在于要分情况讨论.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
3.下列四个函数图象中,当x>0时,y随x的增大而减小的是( )
| A. | 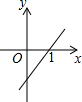 | B. | 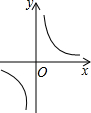 | C. | 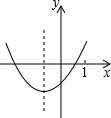 | D. | 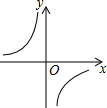 |
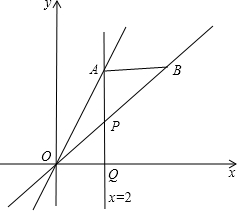 已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).
已知:直线y=2x与x=2相交于点A,直线x=2与x轴相交于点Q,点P是射线AQ上的一点,点B是直线OP上的一点,设AP=t,点B的坐标为(a,b).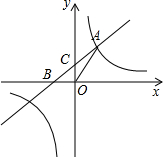 如图,直线y=x+b与双曲线y=$\frac{m}{x}$都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
如图,直线y=x+b与双曲线y=$\frac{m}{x}$都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.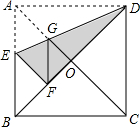 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )


