题目内容
17.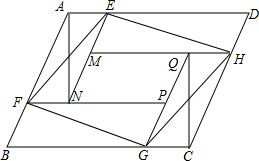 如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$.
如图,有八个全等的三角形拼成一个大四边形ABCD和中间一个小四边形MNPQ,连接EF、GH得到四边形EFGH,设S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,则S2=$\frac{10}{3}$.
分析 根据图形的特征设出四边形MNPQ的面积设为x,将其余八个全等的三角形面积一个设为y,从而用x,y表示出S1,S2,S3,得出答案即可.
解答 解:将四边形MNPQ的面积设为x,将其余八个全等的三角形面积一个设为y,
∵S四边形ABCD=S1,S四边形EFGH=S2,S四边形MNPQ=S3,若S1+S2+S3=10,
∴得出S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=10,故3x+12y=10,
∴x+4y=$\frac{10}{3}$
S2=x+4y=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 此题主要考查了平行四边形的性质,图形面积关系,根据已知得出用x,y表示出S1,S2,S3,再利用S1+S2+S3=10求出是解决问题的关键.

练习册系列答案
相关题目
12.已知一个二元一次方程组的解是$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,则这个方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=-3}\\{xy=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=-3}\\{x-2y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x=y}\\{y-x=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{2}{3x}-\frac{5}{6y}=1}\\{2x+y=-4}\end{array}\right.$ |
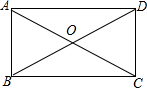 如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4.
如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4.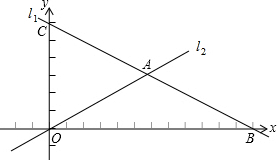 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.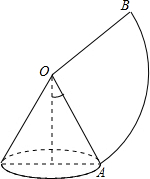 如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12.
如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12. 如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺.
如图,李叔叔想要检测雕塑底座正面的AD和BC是否分别垂直于底边AB,但他随身只带了有刻度的卷尺.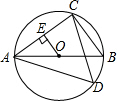 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.