题目内容
8．
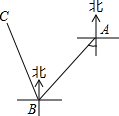一艘轮船由海平面上A地出发向南偏西40°的方向行驶80海里到达B地，再由B地向北偏西20°的方向行驶80海里到达C地，则A，C两地相距（ ）| A． | 100海里 | B． | 80海里 | C． | 60海里 | D． | 40海里 |
分析 先求得∠CBA=60°，然后可判断△ABC为等边三角形，从而可求得AC的长．
解答 解：如图所示：连接AC．
∵点B在点A的南偏西40°方向，点C在点B的北偏西20°方向，
∴∠CBA=60°．
又∵BC=BA，
∴△ABC为等边三角形．
∴AC=BC=AB=80海里．
故选：B．
点评 本题主要考查的是方向角、等边三角形的性质可判断，证得三角线ABC为直角三角形是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．
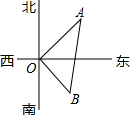如图，在水塔O的东北方向32m处有一抽水站A，在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为（ ）
如图，在水塔O的东北方向32m处有一抽水站A，在水塔的东南方向24m处有一建筑工地B，在AB间建一条直水管，则水管的长为（ ）| A． | 45m | B． | 40m | C． | 50m | D． | 56m |
3．小明第一次向东走40米，第二次向西走30米，第三次向西走40米，最后相当于小明（ ）
| A． | 向西走110米 | B． | 向西走50米 | C． | 向西走30米 | D． | 向东走30米 |
20．已知正方形ABCD，等边三角形PAQ，其中点P在BC上，点Q在CD上，则∠BAP=（ ）
| A． | 10° | B． | 15° | C． | 20° | D． | 30° |
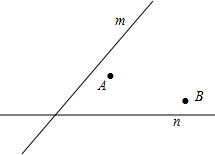如图，移动公司要在S区修建一座信号发射塔，按照设计要求，发射塔到两个城镇A、B的距离相等，到两条高速公路m和n的距离也相等，请用尺规作图法作出发射塔P的位置．（保留作图痕迹）
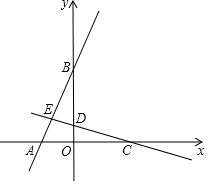如图，在平面直角坐标系中，直线y=mx+4与x，y轴分别交于A，B两点，直线y=-$\frac{1}{3}$x+n与x，y轴分别交于C，D两点，点E（-$\frac{9}{7}$，$\frac{10}{7}$）是这两条直线的交点．