题目内容
12.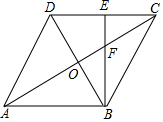 已知:如图,菱形ABCD,对角线AC、BD交于点O,BE⊥DC,垂足为点E,交AC于点F.求证:
已知:如图,菱形ABCD,对角线AC、BD交于点O,BE⊥DC,垂足为点E,交AC于点F.求证:(1)△ABF∽△BED;
(2)$\frac{AC}{BE}$=$\frac{BD}{DE}$.
分析 (1)由菱形的性质得出AC⊥BD,AB∥CD,得出△ABF∽△CEF,由互余的关系得:∠DBE=∠FCE,证出△BED∽△CEF,即可得出结论;
(2)由平行线得出$\frac{AC}{BE}=\frac{AF}{BF}$,由相似三角形的性质得出$\frac{BD}{DE}=\frac{AF}{BF}$,即可得出结论.
解答 证明:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴△ABF∽△CEF,
∵BE⊥DC,
∴∠FEC=∠BED,
由互余的关系得:∠DBE=∠FCE,
∴△BED∽△CEF,
∴△ABF∽△BED;
(2)∵AB∥CD,
∴$\frac{AF}{AC}=\frac{BF}{BE}$,
∴$\frac{AC}{BE}=\frac{AF}{BF}$,
∵△ABF∽△BED,
∴$\frac{BD}{DE}=\frac{AF}{BF}$,
∴$\frac{AC}{BE}$=$\frac{BD}{DE}$.
点评 本题考查了菱形的性质、相似三角形的判定与性质、平行线分线段成比例定理;熟练掌握菱形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.如果把一个锐角△ABC的三边的长都扩大为原来的3倍,那么锐角A的余切值( )
| A. | 扩大为原来的3倍 | B. | 缩小为原来的$\frac{1}{3}$ | C. | 没有变化 | D. | 不能确定 |
 如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.
如图,D为△ABC的边AB上一点,如果∠ACD=∠ABC时,那么图中AC是AD和AB的比例中项.