题目内容
19. 把一张边长为40cm的正方形硬纸板,进行适当地裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
把一张边长为40cm的正方形硬纸板,进行适当地裁剪,折成一个长方体盒子(纸板的厚度忽略不计).(1)如图,若将正方形硬纸板的四角各剪掉一个同样大小的正方形,剩余部分折成一个无盖的长方体盒子,要使折成的长方体盒子的底面积为484cm2,则剪掉的正方形的边长为多少?
(2)若将正方形硬纸板的四周剪掉一些长方形(即剪掉的长方形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子,折成的一个长方体盒子的表面积为550cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
分析 (1)设剪掉的正方形的边长为xcm,根据题意得出(40-2x)2=484,求出即可;
(2)设剪掉的长方形盒子的高为xcm,利用折成的一个长方形盒子的表面积为550cm2,列出方程,求解即可.
解答 解:(1)设剪掉的正方形的边长为xcm,根据题意得:
(40-2x)2=484,
解得x1=31(不合题意,舍去),x2=9,
答:剪掉的正方形的边长为9cm;
(2)设剪掉的长方形盒子的高为xcm,则长为40-2x,宽为20-x,
表面积为:2(40-2x)(20-x)+2x(20-x)+2x(40-2x)=550,
解得:x1=-35(不合题意,舍去),x2=15,
即剪掉的长方形盒子的高为15cm,
则长为:40-2x=40-2×15=10(cm),
宽为:20-x=20-15=5(cm),
此时长方体盒子的长为10cm,宽为5cm,高为15cm.
点评 本题考查了一元二次方程的应用,解答本题的关键是仔细审题,建立数学模型,利用所学知识求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (π-3.14)0=1 | C. | ($\frac{1}{2}$)-1=-2 | D. | $\sqrt{9}$=±3 |
6.在2、0、-1、3这四个数中,最小的数是( )
| A. | 2 | B. | 0 | C. | -1 | D. | 3 |

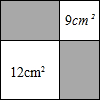 如图,从一个正方形中截取面积为9cm2或12cm2的两个小正方形,则留下阴影部分的面积为12$\sqrt{3}$cm2.
如图,从一个正方形中截取面积为9cm2或12cm2的两个小正方形,则留下阴影部分的面积为12$\sqrt{3}$cm2.