题目内容
1.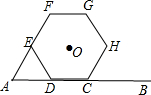 如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.
如图,已知线段AB=10,点D从A点开始沿AB边向右运动,以AD为边向上作正△ADE,再以DE为边向右作正六边形DEFGHC,点C恰好落在线段AB上,当C与B重合时运动结束,则正六边形的中心O的运动路径长为5$\sqrt{3}$,点B与点O的最短距离为5.
分析 作出符合条件的图形,连接OD,证明三角形AOB为直角三角形,根据直角三角形的性质和勾股定理求出答案.
解答  解:如图,连接OD,
解:如图,连接OD,
∵正六边形DEFGHC,
∴△ODB是等边三角形,
∴∠ODB=∠OBD=60°,又OD=OA,
∴∠DAO=∠DOA=30°,
∴∠AOB=90°,又AB=10,
∴OA=5$\sqrt{3}$,OB=5,
故答案为5$\sqrt{3}$;5.
点评 本题考查的是正多边形和圆的知识以及点的轨迹,找出点的移动轨迹、掌握正多边形和圆的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列命题是假命题的是( )
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 对角线互相垂直的四边形是正方形 |
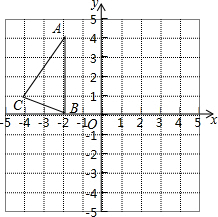 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题: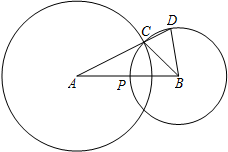 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
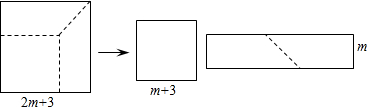
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y. 如图,图中的阴影部分表示什么数?你能写出3个符合要求的数吗?
如图,图中的阴影部分表示什么数?你能写出3个符合要求的数吗?