题目内容
15.(1)解方程组$\left\{\begin{array}{l}{\frac{x+y}{4}+\frac{x-y}{2}=\frac{7}{2}}\\{3(x+y)+2(x-y)=10}\end{array}\right.$(2)解不等式组$\left\{\begin{array}{l}{4x-3<3(2x+1)}\\{\frac{1}{2}x-1>5-\frac{3}{2}x}\end{array}\right.$,并在数轴上画出它的解集.
分析 (1)将原方程组整理成一般式,再利用加减消元法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原方程组整理可得:$\left\{\begin{array}{l}{3x-y=14}&{①}\\{5x+y=10}&{②}\end{array}\right.$,
①+②,得:8x=24,
解得:x=3,
将x=3代入②,得:15+y=10,
解得:y=-5,
则原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$;
(2)解不等式4x-3<3(2x+1),得:x>-3,
解不等式$\frac{1}{2}$x-1>5-$\frac{3}{2}$x,得:x>3,
∴不等式组的解集为x>3,
将解集表示在数轴上如下:
点评 本题考查的是解二元一次方程组和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则及加减消元法是解答此题的关键.

练习册系列答案
相关题目
5.已知a=(-2)0,b=($\frac{1}{2}$)-1,c=(-2)-2,那么a、b、c的大小关系为( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | b>a>c |
10.能和正十二边形组合铺满地面的是( )
| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正三角形 |
20.已知一个几何体的三种视图如图所示,则该几何体是( )


| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
4.若点P在直线y=2x+3上,则点P的坐标可以是( )
| A. | (1,5) | B. | (0,2) | C. | (-1,0) | D. | (1,-1) |
 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的左视图是( )
如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的左视图是( )



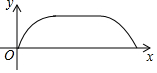
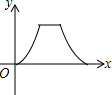
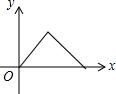
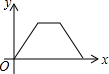
 如图,点E为菱形ABCD边上的一个动点,并延A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( )
如图,点E为菱形ABCD边上的一个动点,并延A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( )