题目内容
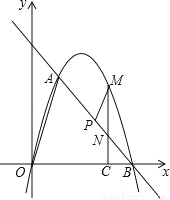
如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx2+nx相交于A（1，3 ），B（4，0）两点．
（1）求出抛物线的解析式；
（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN，求出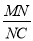
的值，并求出此时点M的坐标．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
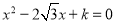有两个相等的实数根，则k值为_____．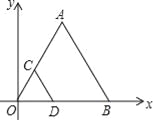
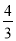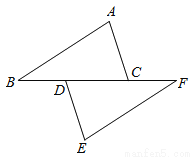
x的图象经过点A，点A的纵坐标为4，反比例函数y=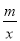
的图象也经过点A，第一象限内的点B在这个反比例函数的图象上，过点B作BC∥x轴，交y轴于点C，且AC=AB．求：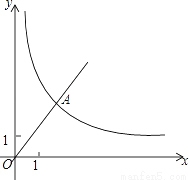
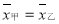，方差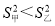
，则成绩较稳定的同学是 （填“甲”或“乙”）.
）
， 
， 
， 
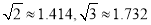．将它们背面朝上洗匀后，从中随机抽取一张卡片，则其正面的数比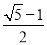
小的概率是__________．