Question

在锐角△ABC中，直线l为BC的中垂线，直线m为∠ABC的角平分线，且l与m相交于点P．若∠A=60°，∠ACP=24°，求∠ABP的度数．

Answer 1

考点：线段垂直平分线的性质

专题：

分析：由线段垂直平分线的性质及角平分线的定义可得到∠ABP=∠CBP=∠BCP，在锐角△ABC中，由三角形内角和定理可得到3∠ABP+∠A+∠ACP=180°，再把已知条件代入可求得∠ABP．

解答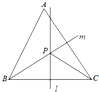：解：∵直线m为∠ABC的角平分线，
∴∠ABP=∠CBP，
∵直线l为BC的中垂线，
∴PB=PC，
∴∠CBP=∠BCP，
∴∠ABP=∠CBP=∠BCP，
在锐角△ABC中，3∠ABP+∠A+∠ACP=180°，
又∵∠A=60°，∠ACP=24°，
∴∠ABP=32°．

点评：本题主要考查线段垂直平分线的性质，根据线段垂直平分线的性质及三角形内角和定理得到3∠ABP+∠A+∠ACP=180°是解题的关键．