题目内容
（1）计算：
+
-
（2）化简求值：当a=2-
，b=
时，求代数式a2+b2-4a+2003的值．
| 12 |
|
| 48 |
（2）化简求值：当a=2-
| 13 |
| 2 |
考点：二次根式的化简求值
专题：
分析：（1）首先化简二次根式进而合并同类二次根式得出即可；
（2）首先借助完全平方公式将原式变形，进而代入求出即可．
（2）首先借助完全平方公式将原式变形，进而代入求出即可．
解答：解：
（1）
+
一
=2
+
-4
=-
；
（2）a2+b2-4a+2003
=（a-2）2+b2+1999
将a=2-
，b=
代入上式得：
原式=（a-2）2+b2+1999
=（2-
-2）2+（
）2+1999
=13+2+1999
=2014．
（1）
| 12 |
|
| 48 |
=2
| 3 |
| ||
| 3 |
| 3 |
=-
| 5 |
| 3 |
| 3 |
（2）a2+b2-4a+2003
=（a-2）2+b2+1999
将a=2-
| 13 |
| 2 |
原式=（a-2）2+b2+1999
=（2-
| 13 |
| 2 |
=13+2+1999
=2014．
点评：此题主要考查了二次根式的化简求值以及整式的化简求值，正确利用完全平方公式是解题关键．
练习册系列答案
相关题目
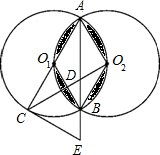如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心，顺次连接A、O1、B、O2．