题目内容
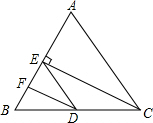 如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.
如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.考点:平行线的判定与性质,垂线
专题:证明题
分析:可先证明AC∥DE,结合平行线的性质可得到∠ACB=∠EDB,再利用角平分线的定义可证得∠BDF=∠BCE,可判定CE∥DF,可得到∠DFB=∠CEF,可证得结论.
解答:证明:
∵∠BED=∠A,
∴AC∥DE,
∴∠ACB=∠BDE,
∵CE平分∠ACB,DF平分∠BDE,
∴∠BDF=
∠BDE,∠BCE=
∠ACB,
∴∠BDF=∠BCE,
∴DF∥CE,
∵CE⊥AB,
∴∠BFD=∠BEC=90°,
∴DF⊥AB.
∵∠BED=∠A,
∴AC∥DE,
∴∠ACB=∠BDE,
∵CE平分∠ACB,DF平分∠BDE,
∴∠BDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BDF=∠BCE,
∴DF∥CE,
∵CE⊥AB,
∴∠BFD=∠BEC=90°,
∴DF⊥AB.
点评:本题主要考查平行线的性质和判定,掌握两直线平行的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行.

练习册系列答案
相关题目
 已知:如图,在?ABCD中,AC、BD相交于点O,点E、F分别在OB、OD上,且OE=OF.求证:四边形AECF是平行四边形.
已知:如图,在?ABCD中,AC、BD相交于点O,点E、F分别在OB、OD上,且OE=OF.求证:四边形AECF是平行四边形.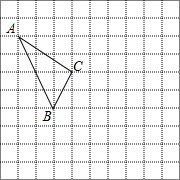 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,3),(2,-1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,3),(2,-1). 如图,两个圆的圆心相同,它们的面积分别是12.56和25.12,求圆环的宽度d(π取3.14,结果保留小数点后两位).
如图,两个圆的圆心相同,它们的面积分别是12.56和25.12,求圆环的宽度d(π取3.14,结果保留小数点后两位).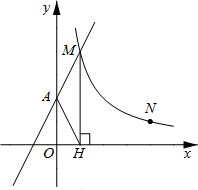 如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=
如图,直线y1=2x+2与y轴交于A点,与反比例函数y2= 以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.
以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.