题目内容
 如图,在?ABCD中,点E,F在AD,BC上,且AE=CF,AF与BE交于点M,CE与DF交于点N,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,点E,F在AD,BC上,且AE=CF,AF与BE交于点M,CE与DF交于点N,求证:四边形EMFN是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:可先证明四边形AECF为平行四边形,可得到AF∥CE,同理可证明四边形BEDF为平行四边形可得到BE∥DF,可证得结论.
解答:证明:∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
∵AE=FC,
∴四边形AECF为平行四边形,
∴AF∥CE,
同理可得四边形BEDF为平行四边形,
∴BE∥DF,
∴四边形EMFN是平行四边形.
∴AD∥BC,且AD=BC,
∵AE=FC,
∴四边形AECF为平行四边形,
∴AF∥CE,
同理可得四边形BEDF为平行四边形,
∴BE∥DF,
∴四边形EMFN是平行四边形.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
若
=
,那么a:b的值是( )
| a+b |
| a |
| 5 |
| 3 |
| A、3:2 | B、2:3 |
| C、C、3:5 | D、D、5:3 |
 如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?
如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?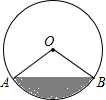 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?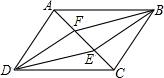 已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由.
已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由.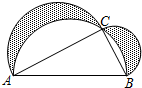 如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.
如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.