题目内容
3. 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠BAC+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=$\frac{1}{2}$∠ACD,∠PBC=$\frac{1}{2}$∠ABC,然后整理得到∠PCD=40°+$\frac{1}{2}$∠ABC,再代入数据计算即可得解.
解答 解:在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,
∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=$\frac{1}{2}$∠ACD,∠PBC=$\frac{1}{2}$∠ABC,
∴∠PCD=∠BPC+∠PBC=40°+$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠ACD=$\frac{1}{2}$∠ABC+40°,
∴∠ACD-∠ABC=80°,
∴∠BAC=∠ACD-∠ABC=80°,
即∠CAB=80°.
点评 本题考查了三角形内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记定理与性质并求出∠PCD=40°+$\frac{1}{2}$∠ABC是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
11.抛物线y=(x+1)2-2的对称轴是( )
| A. | 直线x=1 | B. | 直线x=3 | C. | 直线x=-1 | D. | 直线x=-3 |
18.在时刻8:40,时钟上的时针和分针之间的夹角为( )
| A. | 15° | B. | 20° | C. | 25° | D. | 10° |
15.某商品按进价的100%加价出售,经过一段时间,商家为减少库存,决定以7折销售,这时每件商品( )
| A. | 赚40% | B. | 赔30% | C. | 赔40% | D. | 不赔不赚 |
13.已知x-$\frac{1}{x}$=4,则x2+$\frac{1}{{x}^{2}}$的值为( )
| A. | 6 | B. | 16 | C. | 14 | D. | 18 |
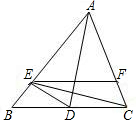 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).