题目内容
13.在数学实验课上,李静同学剪了两张直角三角形纸片,进行了如下的操作: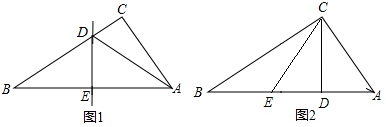
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为12cm;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为36°;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.
分析 操作一:(1)由翻折的性质可知:BD=AD,于是AD+DC=BC,从而可知△ACD的周长=BC+AC;
(2)设∠CAD=x,则∠BAD=2x,由翻折的性质可知∠CBA=2x,然后根据直角三角形两锐角互余可知:x+2x+2x=90°.
操作二:先利用勾股定理求得AC的长,然后利用面积法求得DC的长,在Rt△ACD中,利用勾股定理可求得AD的长,由翻折的性质可知:DE=DA,最后根据BE=AB-DE-AD计算即可.
解答 解:操作一:(1)翻折的性质可知:BD=AD,
∴AD+DC=BC=7.
∴△ACD的周长=CD+AD+AC=BC+AC=7+5=12cm.
故答案为:12cm.
(2)设∠CAD=x,则∠BAD=2x.
由翻折的性质可知:∠BAD=∠CBA=2x,
∵∠B+∠BAC=90°,
∴x+2x+2x=90°.
解得;x=18°.
∴2x=2×18°=36°.
∴∠B=36°.
故答案为:36°.
操作二:在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6.
由翻折的性质可知:ED=AD,DC⊥AB.
∵${S}_{△ABC}=\frac{1}{2}AC•BC=\frac{1}{2}AB•CD$,
∴10CD=6×8.
∴CD=4.8.
在Rt△ADC中,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{6}^{2}-4.{8}^{2}}$=3.6.
∴EA=3.6×2=7.2.
∴BE=10-7.2=2.8.
点评 本题主要考查的是翻折的性质、勾股定理的应用,利用面积法求得CD的长度是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
5.数学翻译 牛顿是举世闻名的伟大数学家、物理学家,他创立了微积分(另一个创立者是莱布尼茨)、经典力学,在代数学、光学、天文学等方面也作出了重要贡献,牛顿用数学的语言、方法描述和研究自然规律,他呕心沥血,写成的光辉著作《自然哲学的数学原理》,照亮了人类科学文明的大道,牛顿在他的《普遍的算术》一书中写道:“要解答一个含有数量间的抽象关系的问题,只要把题目由日常的语言译成代数的语言就行了.”下表是由牛顿给出的1个例子改写、简化而成的,请将表的空白补上(不必化简).
根据上表中的(3)可解得x=400.
| 日常语言 | 代数语言 |
| 一个商人有一笔钱 | x |
| 第一年他花去了100镑 | x-100 |
| 补进去余额的$\frac{1}{3}$ | (x-100)+$\frac{1}{3}$(x-100) |
| 第二年他又花去了100镑 | (1)(x-100)+$\frac{1}{3}$(x-100)-100 |
| 又补进去余额的$\frac{1}{3}$ | (2)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100] |
| 结果他的钱数正好是原来的钱数 | (3)(x-100)+$\frac{1}{3}$(x-100)-100+$\frac{1}{3}$[(x-100)+$\frac{1}{3}$(x-100)-100]=x |
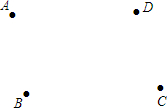 如图,A,B,C,D是四个鱼塘的位置,要用一个供水泵向这四个鱼塘供水,为了使供水管最短,供水泵应建在什么位置?画出图形并说明理由.
如图,A,B,C,D是四个鱼塘的位置,要用一个供水泵向这四个鱼塘供水,为了使供水管最短,供水泵应建在什么位置?画出图形并说明理由.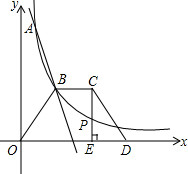 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点,
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)(x>0)的图象交于A(1,6),B(a,3)两点, 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.