题目内容
11. 直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.
直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.
分析 先根据图象判断出a的符号,再根据绝对值的性质去掉绝对值符号即可.
解答 解:根据图象可知直线y=(2-a)x+3-a经过第二、三、四象限,
所以2-a<0,3-a<0,
∴|3-a|+|2-a|=a-3+a-2=2a-5.
故答案为:2a-5.
点评 本题主要考查了一次函数的图象性质及绝对值的性质,掌握一次函数的图象与系数的关系是解答此题的关键.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
相关题目
20.一次函数y=-2x+b的图象上有一点A(4,-3),则b的值为( )
| A. | 5 | B. | 3 | C. | -3 | D. | -5 |
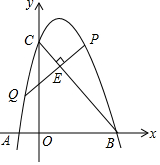 抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.
抛物线y=ax2+bx+4交x轴于点A(-1,0),B(3,0),交y轴于点C,点E为BC上的点,过点E的垂线交抛物线于点P,Q,点P在第一象限,若点E为PQ的中点,求点P的坐标.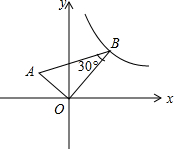 如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=$\frac{3}{x}$的图象上,求过点A的反比例函数的解析式.
如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=$\frac{3}{x}$的图象上,求过点A的反比例函数的解析式.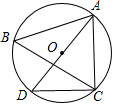 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,∠B=70°,则∠DAC=20°.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,∠B=70°,则∠DAC=20°.