题目内容
14.某内陆城市为了落实国家“一带一路”战略,促进经济发展,增强对外贸易的竞争力,把距离港口420km的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2h,求汽车原来的平均速度.分析 求的汽车原来的平均速度,路程为420km,一定是根据时间来列等量关系,本题的关键描述语是:从甲地到乙地的时间缩短了2h.等量关系为:原来时间-现在时间=2.
解答 解:设汽车原来的平均速度是x km/h,
根据题意得:$\frac{420}{x}$-$\frac{420}{(1+50%)x}$=2,
解得:x=70
经检验:x=70是原方程的解.
答:汽车原来的平均速度70km/h.
点评 本题考查了分式方程的应用.应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如图是一个几何体的三视图,则这个几何体是( )


| A. | 三棱柱 | B. | 圆柱 | C. | 圆台 | D. | 圆锥 |
2.下列几何体中,其主视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.我市某连续7天的最高气温为:28°,27°,30°,33°,30°,30°,32°,这组数据的平均数和众数分别是( )
| A. | 28°,30° | B. | 30°,28° | C. | 31°,30° | D. | 30°,30° |
10.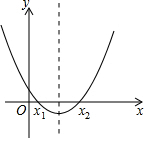 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
 函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )
函数y=kx2-kx+m(k,m都是常数且k≠0)的图象如上图,如果x=a时,y<0,那么x=a-1时,函数值( )| A. | y=m | B. | y<0 | C. | y>m | D. | 0<y<m |
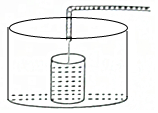 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )


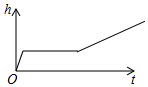
 直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.
直线y=(2-a)x+3-a在直角坐标系中的图象如图所示,化简|3-a|+|2-a|=2a-5.