题目内容
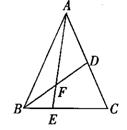
如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE,若△ABC的面积为18,给出下列命题:①△ABE的面积为6;②△ABF的面积和四边形DFEC的面积相等;③点F是BD的中点;④四边形DFEC的面积为 .其中,正确的结论有 .(把你认为正确的结论的序号都填上)
.其中,正确的结论有 .(把你认为正确的结论的序号都填上)
①、③、④.
【解析】①∵△ABC的面积为18,EC=2EB,∴△ABE的面积=18× =6,故①正确
=6,故①正确 ;
;
②∵EC=2EB,点D是AC的中点,∴△ABE的面积≠△BCD的面积,∴△ABF的面积和四边形DFEC的面积不相等,故②错误;
③过D点作DG∥BC,∵点D是AC的中点,∴DG=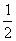 EC, ∵EC=2EB, ∴DG=BE, ∵DG∥BC,∴∠DGF=∠BEF,∠GDF=∠EBF, 在△DGF与△BEF中,∠DGF=∠BEF, DG=BE ,∠GDF=∠EBF,∴△DGF≌△BEF(ASA), ∴DF=BF, ∴点F是BD的中点,故③正确;
EC, ∵EC=2EB, ∴DG=BE, ∵DG∥BC,∴∠DGF=∠BEF,∠GDF=∠EBF, 在△DGF与△BEF中,∠DGF=∠BEF, DG=BE ,∠GDF=∠EBF,∴△DGF≌△BEF(ASA), ∴DF=BF, ∴点F是BD的中点,故③正确;
④四边形DFEC的面积=18-18× -18×
-18×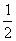 ×
×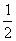 =18-6-
=18-6-
 =,故④正确.
=,故④正确.
故正确的结论有①③④.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


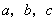 的值,使二次函数
的值,使二次函数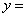
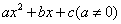 的图象同时足下列条件:①开口向下,②当x<-2时,
的图象同时足下列条件:①开口向下,②当x<-2时,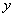 随
随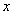 的增大而增大;当x>-2时,
的增大而增大;当x>-2时,
 ,则一次函数
,则一次函数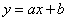 与反比例函数
与反比例函数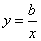 在同一直角坐标系中的图象大致可能是( )
在同一直角坐标系中的图象大致可能是( ) B.
B. C.
C. D.
D.