题目内容
将甲、乙、丙3人等可能地分配到3个房间中去,则每个房间恰有1人的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:根据甲、乙、丙三人被分配到三个房间都具有三种可能求出总情况数,再确定出每个房间恰好有1人的情况数,然后概率公式列式进行计算即可得解.
解答:解:∵甲、乙、丙被分配到3个房间都有3种可能情况,
∴总情况数为3×3×3=27,
每个房间恰有1人共有:(甲、乙、丙),(甲、丙、乙),(乙、甲、丙),(乙、丙、甲),(丙、甲、乙),(丙、乙、甲)6种情况,
所以,P(每个房间恰有1人)=
=
.
故选B.
∴总情况数为3×3×3=27,
每个房间恰有1人共有:(甲、乙、丙),(甲、丙、乙),(乙、甲、丙),(乙、丙、甲),(丙、甲、乙),(丙、乙、甲)6种情况,
所以,P(每个房间恰有1人)=
| 6 |
| 27 |
| 2 |
| 9 |
故选B.
点评:本题考查了概率公式,根据三个人的等可能性确定出所有的可能情况数是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知抛物线y=x2-2x,下列说法中错误的是( )
| A、该抛物线的对称轴是直线x=1 |
| B、该抛物线的顶点在第三象限 |
| C、该抛物线的开口向上 |
| D、该抛物线经过原点 |
 如图,Rt△ABC中,∠A=90°,它的面积为
如图,Rt△ABC中,∠A=90°,它的面积为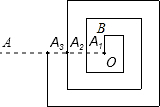 如图是一个回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3…若从O到点A1的回形线为第一圈(长为7),从点A1到A2为第二圈,…以此类推,则第10圈的线长为( )
如图是一个回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3…若从O到点A1的回形线为第一圈(长为7),从点A1到A2为第二圈,…以此类推,则第10圈的线长为( )