题目内容
20.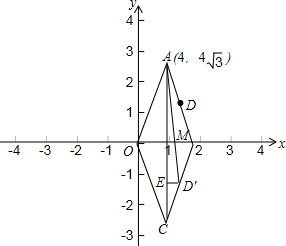 如图,直角坐标系中,四边形ABCO是菱形,对角线OB在x轴正半轴上,点A的坐标为(4,4$\sqrt{3}$),点D为AB的中点.动点M从点O出发沿x轴向点B运动,运动的速度为每秒1个单位,试解答下列问题:
如图,直角坐标系中,四边形ABCO是菱形,对角线OB在x轴正半轴上,点A的坐标为(4,4$\sqrt{3}$),点D为AB的中点.动点M从点O出发沿x轴向点B运动,运动的速度为每秒1个单位,试解答下列问题:(1)则菱形ABCO的周长为32,菱形ABCO的周长为32,
(2)当t=4时,求MA+MD的值;
(3)当t取什么值时,使MA+MD的值最小?并求出他的最小值.
分析 (1)根据坐标与图形的关系求出OF,AF的长,根据勾股定理求出菱形的边长,根据菱形的性质求出周长;
(2)根据直角三角形的斜边的中线是斜边的一半求出MD的值,计算得到MA+MD的值;
(3)作点D关于x轴的对称点D′,连接AD′交x轴于点M,作出MA+MD的值最小时的点M,根据菱形的性质和坐标与图形的关系求出AD′的长,得到答案.
解答 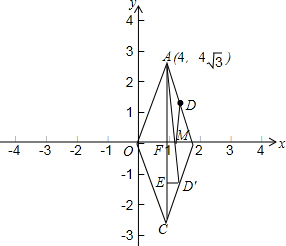 解:(1)∵点A的坐标为(4,4$\sqrt{3}$),
解:(1)∵点A的坐标为(4,4$\sqrt{3}$),
∴OF=4,AF=4$\sqrt{3}$,
由勾股定理得,OA=$\sqrt{O{F}^{2}+A{F}^{2}}$=8,
∴菱形ABCO的周长为32;
(2)当t=4时,点M与对角线的交点F重合,则MA=4$\sqrt{3}$,
在Rt△AMB中,AB=8,点D为AB的中点,
∴MD=$\frac{1}{2}$AB=4,
∴MA+MD=4$\sqrt{3}$+4;
(3)作点D关于x轴的对称点D′,连接AD′交x轴于点M,
则此时MA+MD的值最小,
由题意和菱形的性质可知,点D的坐标为(6,2$\sqrt{3}$),
则D′的坐标为(6,-2$\sqrt{3}$),
设直线AD′的解析式为:y=kx+b,
$\left\{\begin{array}{l}{4k+b=4\sqrt{3}}\\{6k+b=-2\sqrt{3}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-3\sqrt{3}}\\{b=16\sqrt{3}}\end{array}\right.$,
则直线AD′的解析式为:y=-3$\sqrt{3}$x+16$\sqrt{3}$,
-3$\sqrt{3}$x+16$\sqrt{3}$=0,x=$\frac{16}{3}$,
点M的坐标为($\frac{16}{3}$,0),即OM=$\frac{16}{3}$,
则当t=$\frac{16}{3}$时,MA+MD的值最小,
作D′E⊥AC于E,
由菱形的性质可知,D′为BC的中点,
∴D′E=2,EF=2$\sqrt{3}$,则AE=6$\sqrt{3}$,
在Rt△AED′中,AE=6$\sqrt{3}$,D′E=2,
AD′=$\sqrt{D′{E}^{2}+A{E}^{2}}$=4$\sqrt{7}$,
则MA+MD的最小值为4$\sqrt{7}$.
点评 本题考查的是菱形的性质、勾股定理和轴对称-最短路径问题以及待定系数法求一次函数解析式,灵活应用待定系数法求函数解析式、掌握直角三角形的斜边的中线是斜边的一半,作出对称点得到最短路径是解题的关键.

| A. | -4 | B. | -2 | C. | 2 | D. | 0 |
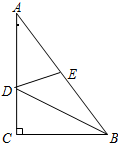 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )| A. | $\frac{\sqrt{10}}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{3}{2}$ |
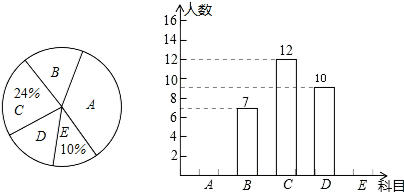
| A. | 选科目E的有5人 | |
| B. | 选科目D的扇形圆心角是72° | |
| C. | 选科目A的人数占体育社团人数的一半 | |
| D. | 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6° |
 如图,已知l3∥l4∥l5,它们依次交直线l1、l2于点E、A、C和点D、A、B,如果AD=2,AE=3,AB=4,那么CE=9.
如图,已知l3∥l4∥l5,它们依次交直线l1、l2于点E、A、C和点D、A、B,如果AD=2,AE=3,AB=4,那么CE=9. 下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.
下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.