题目内容
求所有的三元数组(m,n,p),使其满足pn+144=m2,其中m,n是正整数,p是质数.
考点:质数与合数
专题:
分析:由pn+144=m2,可得pn=m2-144=(m+12)(m-12),根据p是质数,可设m-12=pk,则m+12=pn-k,得到pn-k-pk=24,pk(pn-2k-1)=3×23,得到pk=3,pn-2k-1=23或pk=23,pn-2k-1=3,进一步得到关于m,n,p的方程求解即可.
解答:解:由pn+144=m2,
pn=m2-144=(m+12)(m-12),
∵p是质数,
∴设m-12=pk,则m+12=pn-k,
∴pn-k-pk=24,
∴pk(pn-2k-1)=3×23,
∴pk=3,pn-2k-1=23,
解得p=3,k=1,n=4,
∴m=pk+12=15,
或pk=23,pn-2k-1=3,
解得p=2,k=3,n=8,
∴m=pk+12=20,
∴所有三元数组为(15,4,3)或(20,2,8).
pn=m2-144=(m+12)(m-12),
∵p是质数,
∴设m-12=pk,则m+12=pn-k,
∴pn-k-pk=24,
∴pk(pn-2k-1)=3×23,
∴pk=3,pn-2k-1=23,
解得p=3,k=1,n=4,
∴m=pk+12=15,
或pk=23,pn-2k-1=3,
解得p=2,k=3,n=8,
∴m=pk+12=20,
∴所有三元数组为(15,4,3)或(20,2,8).
点评:考查了质数与合数,此题难度比较大,要认真分析题意读懂题意,理解质数的概念.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
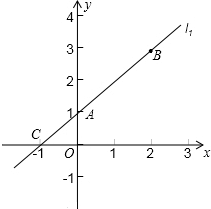 如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0).
如图,已知直线l1经过点A(0,1)与点B(2,3),另一条直线l2经过点B,且与x轴相交于点P(m,0). +(4y2-3xy),其中x=-1,y=-
+(4y2-3xy),其中x=-1,y=-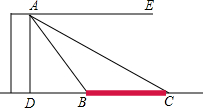 如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)
如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和30°.求BD,BC的长.(结果精确到0.01m)