题目内容
 已知二次函数y=x2-kx+k-1( k>2).
已知二次函数y=x2-kx+k-1( k>2).(1)求证:抛物线y=x2-kx+k-1( k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若tan∠OAC=3,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与⊙P相离、相切、相交.
考点:二次函数综合题
专题:
分析:(1)抛物线与x轴有两个交点,通过证明判别式△=b2-4ac>0即可;
(2)根据题意可设A(1,0),C(0,a),根据三角函数可得点C(0,3),再代入即可得到k的值,从而得到抛物线的表达式;
(3)分别根据点P与x轴的距离>1,=1或<1,列出关于m的方程或不等式,进一步得到当m取何值时,x轴与⊙P相离、相切、相交.
(2)根据题意可设A(1,0),C(0,a),根据三角函数可得点C(0,3),再代入即可得到k的值,从而得到抛物线的表达式;
(3)分别根据点P与x轴的距离>1,=1或<1,列出关于m的方程或不等式,进一步得到当m取何值时,x轴与⊙P相离、相切、相交.
解答:解:(1)根据题意有:△=k2-4k+4=(k-2 )2,
∵k>2,
∴△>0,
所以抛物线与x轴必有两个交点.
2)设f(x)=x2-kx+k-1
根据题意知
对称轴x=
>1,且f(1)=0,f(0)=k-1>1
∴可设A(1,0),C(0,a)
在RT△COA中,tan∠OAC=3=
=
,
∴a=3
∴点C(0,3)
把点C代入抛物线求得k=4,
故抛物线的表达式为y=x2-4x+3.
(3)当m2-4m+3=-1,即m=2或m2-4m+3=1,即m=2±
时,x轴与⊙P相切;
当m<2-
或m>2+
时,x轴与⊙P相离;
当2-
<m<2+
且时m≠2,x轴与⊙P相交.
∵k>2,
∴△>0,
所以抛物线与x轴必有两个交点.
2)设f(x)=x2-kx+k-1
根据题意知
对称轴x=
| k |
| 2 |
∴可设A(1,0),C(0,a)
在RT△COA中,tan∠OAC=3=
| OC |
| OA |
| a |
| 1 |
∴a=3
∴点C(0,3)
把点C代入抛物线求得k=4,
故抛物线的表达式为y=x2-4x+3.
(3)当m2-4m+3=-1,即m=2或m2-4m+3=1,即m=2±
| 2 |
当m<2-
| 2 |
| 2 |
当2-
| 2 |
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:判别式,三角函数,待定系数法求函数解析式,方程思想,直线与圆的位置关系,综合性较强,有一定的难度.

练习册系列答案
相关题目
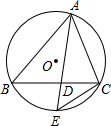 如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )| A、3个 | B、2个 | C、1个 | D、0个 |
 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.