题目内容
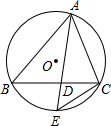 如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )
如图,△ABC的三个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与△ABD相似的三角形有( )| A、3个 | B、2个 | C、1个 | D、0个 |
考点:相似三角形的判定,圆周角定理
专题:
分析:根据同弧所对的圆周角相等,得∠B=∠E,∠BAE=∠BCE,再由角平分线定义,则△ACE∽△ABD,△CDE∽△ABD.
解答:解:与△CAE相似的所有三角形:△DBE,△DAB;
∵∠B=∠E,∠BAE=∠DCE,
∴△ABD∽△CED;
∵∠B=∠E,AD是∠BAC的平分线,
∴∠BAD=∠EAC,
∴△DAB∽△CAE.
综上所述,与△ABD相似的三角形是△ACE∽△ABD,△CDE∽△ABD,共有2个.
故选:B.
∵∠B=∠E,∠BAE=∠DCE,
∴△ABD∽△CED;
∵∠B=∠E,AD是∠BAC的平分线,
∴∠BAD=∠EAC,
∴△DAB∽△CAE.
综上所述,与△ABD相似的三角形是△ACE∽△ABD,△CDE∽△ABD,共有2个.
故选:B.
点评:本题考查了三角形的相似的判定和性质以及圆周角定理,证明此题的关键是利用圆周角定理,再利用角平分线,证出三角形相似.

练习册系列答案
相关题目
下列方程,是一元二次方程的是( )
| A、6x2+7x=20 | ||
| B、2x2-3xy+4=0 | ||
C、2x2-
| ||
| D、x(x-4)+1=x2-2x |
如果二次函数y=(x-h)2+k(hk≠0)的图象经过原点,那么分式
的值是( )
| h2 |
| k |
| A、0 | B、1 | C、-1 | D、0或1 |
下列说法正确的是( )
| A、带根号的数都是无理数 |
| B、不带根号的数都是有理数 |
| C、无理数是无限小数 |
| D、无限小数是无理数 |
已知正△AOB的三个顶点都在抛物线y=
x2上,其中O为坐标原点,则正△AOB的面积为( )
| 1 |
| 2 |
A、4
| ||
B、12
| ||
C、6
| ||
| D、24 |
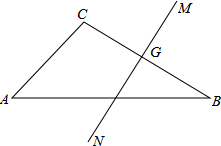 如图,△ABC中,NM是BC边的垂直平分线,垂足为G.
如图,△ABC中,NM是BC边的垂直平分线,垂足为G. 如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E. 已知二次函数y=x2-kx+k-1( k>2).
已知二次函数y=x2-kx+k-1( k>2).