题目内容
已知:⊙O的半径长为5,点A、B、C在⊙O上,AB=BC=6,点E在射线BC上.
(1)如图1,联结AE、CE,求证:AE=CE;
(2)如图2,以点C为圆心,CO为半径画弧交半径OB于D,求BD的长.
(3)当OE=
时,求线段AE的长.

(1)如图1,联结AE、CE,求证:AE=CE;
(2)如图2,以点C为圆心,CO为半径画弧交半径OB于D,求BD的长.
(3)当OE=
| 11 |
| 5 |

考点:圆的综合题
专题:综合题
分析:(1)证明:作OF⊥AB于F,OH⊥BC于H,由AB=BC,根据圆心角、弧、弦、弦心距之间的关系OF=OH,根据角平分线的判定得到BE平分∠ABC,然后利用“SAS”可判断△ABE≌△CBE,则AE=CE;
(2)作CN⊥BE于N,OM⊥BC于M,由OB=OC,根据等腰三角形的性质得BM=CM=
BC=3,在Rt△BMO中,根据勾股定理计算出OM=4,在利用面积法计算出CN=
,
在Rt△OCN中利用勾股定理计算出ON=
,由CD=CN,根据等腰三角形的性质得ON=DN,则BD=OB-2ON=
;
(3)作CN⊥BE于N,由(2)得CN=
,ON=
,分类讨论:当E在OB的延长线上,NE=ON+OE=
,在Rt△CEN中,根据勾股定理计算出CE=6;当E在OB上,即OE′=
,NE′=OE′-ON=
,在Rt△CE′N中,根据勾股定理计算出CE′=
,即CE的长为6或
,由于AE=CE,所以AE的长为6或
.
(2)作CN⊥BE于N,OM⊥BC于M,由OB=OC,根据等腰三角形的性质得BM=CM=
| 1 |
| 2 |
| 24 |
| 5 |
在Rt△OCN中利用勾股定理计算出ON=
| 7 |
| 5 |
| 11 |
| 5 |
(3)作CN⊥BE于N,由(2)得CN=
| 24 |
| 5 |
| 7 |
| 5 |
| 18 |
| 5 |
| 11 |
| 5 |
| 4 |
| 5 |
4
| ||
| 5 |
4
| ||
| 5 |
4
| ||
| 5 |
解答:(1)证明:作OF⊥AB于F,OH⊥BC于H,如图1,
∵AB=BC,
∴OF=OH,
∴BE平分∠ABC,
在△ABE和△CBE中
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:作CN⊥BE于N,OM⊥BC于M,如图2,
∵OB=OC,
∴BM=CM=
BC=3,
在Rt△BMO中,OB=5,BM=3,
∴OM=
=4,
∵
OM•BC=
CN•OB,
∴CN=
=
,
在Rt△OCN中,OC=5,
∴ON=
=
,
∵CO=CD,
∴ON=DN,
∴BD=OB-2ON=5-2×
=
;
(3)解:作CN⊥BE于N,如图,
由(2)得CN=
,ON=
,
当E在OB的延长线上,NE=ON+OE=
+
=
,
在Rt△CEN中,CE=
=
=6;
当E在OB上,即OE′=
,NE′=OE′-ON=
-
=
,
在Rt△CE′N中,CE′=
=
=
,
∴CE的长为6或
,
∵AE=CE,
∴AE的长为6或
.
∵AB=BC,
∴OF=OH,
∴BE平分∠ABC,
在△ABE和△CBE中
|
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:作CN⊥BE于N,OM⊥BC于M,如图2,
∵OB=OC,
∴BM=CM=
| 1 |
| 2 |
在Rt△BMO中,OB=5,BM=3,

∴OM=
| OB2-BM2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CN=
| 4×6 |
| 5 |
| 24 |
| 5 |
在Rt△OCN中,OC=5,
∴ON=
| OC2-CN2 |
| 7 |
| 5 |
∵CO=CD,
∴ON=DN,
∴BD=OB-2ON=5-2×
| 7 |
| 5 |
| 11 |
| 5 |
(3)解:作CN⊥BE于N,如图,
由(2)得CN=
| 24 |
| 5 |
| 7 |
| 5 |
当E在OB的延长线上,NE=ON+OE=
| 7 |
| 5 |
| 11 |
| 5 |
| 18 |
| 5 |
在Rt△CEN中,CE=
| NE2+CN2 |
(
|
当E在OB上,即OE′=
| 11 |
| 5 |
| 11 |
| 5 |
| 7 |
| 5 |
| 4 |
| 5 |
在Rt△CE′N中,CE′=
| NE′2+CN2 |
(
|
4
| ||
| 5 |
∴CE的长为6或
4
| ||
| 5 |
∵AE=CE,
∴AE的长为6或
4
| ||
| 5 |
点评:本题考查了圆的综合题:熟练掌握圆心角、弧、弦、弦心距之间的关系和三角形全等的判定与性质;也考查了分类讨论的思想和勾股定理.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E. 已知二次函数y=x2-kx+k-1( k>2).
已知二次函数y=x2-kx+k-1( k>2).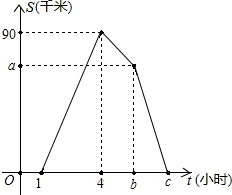 甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.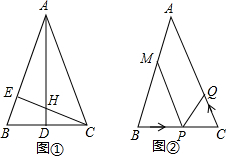 在△ABC中,AB=AC,
在△ABC中,AB=AC, 如图,在△ABC中,∠ACB=90°,AC=8,sinB=
如图,在△ABC中,∠ACB=90°,AC=8,sinB=