题目内容
6.为了丰富群众文化生活,某县城区已经整体转换成了数字电视.目前该县广播电视信息网络公司正在对乡镇进行数字电视改装.公司现有400户申请了但还未安装的用户,此外每天还有新的用户申请.已知每个安装小组每天安装的数量相同,且每天申请安装的用户数也相同,公司若安排3个安装小组同时安装,则50天可以安装完所有新、旧申请用户;若公司安排5个安装小组同时安装,则10天可以安装完所有新,旧申请用户.(1)求每天新申请安装的用户数及每个安装小组每天安装的数量;
(2)如果要求在8天内安装完所有新、旧申请用户,但前3天只能派出2个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
分析 (1)设每天新申请安装的用户数为x个,每个安装小组每天安装的数量为y户,根据3个安装小组同时安装,50天可以安装完所有新、旧申请用户5个安装小组同时安装,则10天可以安装完所有新,旧申请用户,列方程组求解;
(2)设最后几天增加a个小组,根据8天内安装完所有新、旧申请用户,列不等式求解.
解答 解:(1)设每天新申请安装的用户数为x个,每个安装小组每天安装的数量为y户,
由题意得,$\left\{\begin{array}{l}{3y×50=400+50x}\\{5y×10=400+10x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=16}\end{array}\right.$.
答:每天新申请安装的用户数为40个,每个安装小组每天安装的数量为16户;
(2)设最后几天增加a个小组,
由题意得,3×2×16+5×(2+a)×16≥400+8×40,
解得:a≥5.8.
答:至少增加6个小组.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.2014年11月份,某市区一周空气质量报告中某污染指数的数据是:61,75,61,63,50,63,61,则下列表述错误的是( )
| A. | 方差是44 | B. | 众数是61 | C. | 平均数是62 | D. | 中位数是61 |
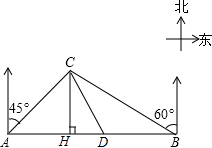 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H. 将两个全等的等腰直角三角形摆成如图所示的样子(图中的所有点,线都在同一平面内),请在图中找出两对相似而不全等的三角形,并说明它们相似的理由.
将两个全等的等腰直角三角形摆成如图所示的样子(图中的所有点,线都在同一平面内),请在图中找出两对相似而不全等的三角形,并说明它们相似的理由. 如图,数轴上有A,B两点,点A运动的速度是每秒2个单位,点B运动的速度是每秒1个单位.
如图,数轴上有A,B两点,点A运动的速度是每秒2个单位,点B运动的速度是每秒1个单位.