题目内容
2.一般的,形如x+$\frac{1}{x}$=a(a是已知数)的分式方程有两个解,通常用x1,x2表示,请你观察下列方程及其解的特征:(1)x+$\frac{1}{x}$=2的解为x1=x2=1;
(2)x+$\frac{1}{x}$=$\frac{5}{2}$的解为x1=2,x2=$\frac{1}{2}$;
(3)x+$\frac{1}{x}$=$\frac{10}{3}$的解为x1=3,x2=$\frac{1}{3}$;
…
猜想:x+$\frac{1}{x}$=$\frac{17}{4}$的解为x1=4,x2=$\frac{1}{4}$;关于x的方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$的解为x1=a,x2=$\frac{a}{a-1}$.
分析 仿照方程解方程,归纳总结得到结果,方程变形后,利用得出的规律得到结果即可.
解答 解:猜想方程x+$\frac{1}{x}$=$\frac{17}{4}$,即方程x+$\frac{1}{x}$=4+$\frac{1}{4}$的解是x1=4,x2=$\frac{1}{4}$;
把方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$变形得,x-1+$\frac{2}{x-1}$=a-1+$\frac{2}{a-1}$,
∴x-1=a-1或x-1=$\frac{1}{a-1}$,
∴x1=a,x2=$\frac{a}{a-1}$.
故答案为$\frac{1}{4}$;x1=a,x2=$\frac{a}{a-1}$.
点评 本题考查了分式方程的解,方程的解即为能使方程左右两边相等的未知数的值.弄清题中的规律是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )| A. | 6 | B. | 16 | C. | 32 | D. | 64 |
10.在△ABC中,∠BAC=90°,AB=3,AC=4,D是BC的中点,则BD的长为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |
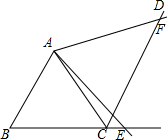 已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.
已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.