题目内容
7．
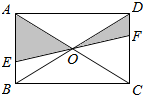如图，EF过矩形ABCD对角线的交点O，并且分别交AB、CD于E、F，那么阴影部分的面积是距形ABCD的面积的多少？
分析 只要证明△AOE≌△COF，即可推出S△AOE=S△COF，推出S阴=S△COD=$\frac{1}{2}$S△ADC=$\frac{1}{4}$S矩形ABCD．
解答 解：∵四边形ABCD是矩形，
∴AB∥DC，OA=OC，
∴∠OAE=∠OCF，
在△AOE和△COF中，
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$，
∴△AOE≌△COF，
∴S△AOE=S△COF，
∴S阴=S△COD=$\frac{1}{2}$S△ADC=$\frac{1}{4}$S矩形ABCD．
点评 本题考查矩形的性质、全等三角形的判定和性质等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
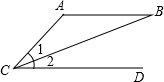如图，有以下3个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这3个条件中任选2个作为题设，另1个作为结论，则组成的命题是真命题的概率是1．
15．下列计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | （-3）2=6 | C． | （-a3）2=a6 | D． | a2+a3=a5 |
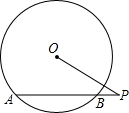如图，⊙O的半径为5，点P是弦AB延长线上的一点，连接OP，若OP=8，∠P=30°，则弦AB的长为6．
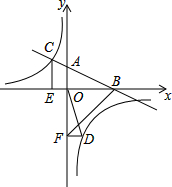如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y=$\frac{k}{x}$（k≠0）的图象在第二象限交于点C，CE⊥x轴，垂足为点E，sin∠ABO=$\frac{\sqrt{5}}{5}$，OB=2，OE=1．
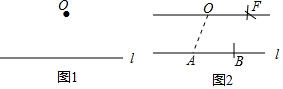下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程．