题目内容
2．
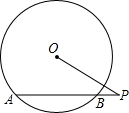如图，⊙O的半径为5，点P是弦AB延长线上的一点，连接OP，若OP=8，∠P=30°，则弦AB的长为6．
分析 作OC⊥AB于C，连结OA，根据垂径定理得AC=BC，由于OP=8，∠P=30°，根据含30度的直角三角形三边的关系得OC=4，然后利用勾股定理可计算出AC，再利用AB=2AC求解．
解答 
解：作OC⊥AB于C，连结OA，如图，
则AC=BC，
∵OP=8，∠P=30°，
∴OC=4，
在Rt△OAC中，OA=5，OC=4，
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=3，
∴AB=2AC=6．
故答案为6．
点评 本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
相关题目
如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，竹条AB的长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则一面贴纸的面积为175πcm2（结果保留π）．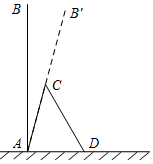
一棵大树AB（假定大树AB垂直于地面）被刮倾斜15°后折断在地上，树的顶部恰好接触到地面D处（如示意图所示），量得大树的倾斜角∠BAC=15°，大树被折断部分和地面所成的角∠ADC=60°，AD=4米，求大树AB原来的高度是多少米？（结果保留整数，参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4）
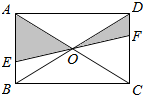如图，EF过矩形ABCD对角线的交点O，并且分别交AB、CD于E、F，那么阴影部分的面积是距形ABCD的面积的多少？
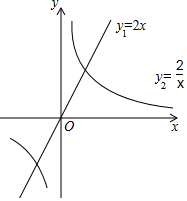在平面直角坐标系xOy中，直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示，小明说：“满足y1＞y2的x的取值范围是x＞1．”你同意他的观点吗？答：不同意．理由是y1＞y2的x的取值范围是x＞1或-1＜x＜0．