题目内容
18.扬州建城2500年之际,为了继续美化城市,计划在路旁栽树1200棵,由于志愿者的参加,实际每天栽树的棵数比原计划多20%,结果提前2天完成,求原计划每天栽树多少棵?分析 设原计划每天种树x棵,则实际每天栽树的棵数为(1+20%),根据题意可得,实际比计划少用2天,据此列方程求解.
解答 解:设原计划每天种树x棵,则实际每天栽树的棵数为(1+20%),
由题意得,$\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=2,
解得:x=100,
经检验,x=100是原分式方程的解,且符合题意.
答:原计划每天种树100棵.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
8.如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112μg/m3;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是( )
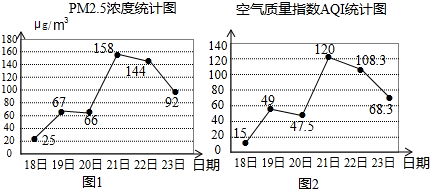

| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
6.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{12}$ | C. | $\sqrt{8}$ | D. | $\sqrt{\frac{1}{2}}$ |
3.已知a+b=3,ab=2,则a2+b2的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
7.下列命题错误的是( )
| A. | 对角线互相垂直平分的四边形是菱形 | |
| B. | 平行四边形的对角线互相平分 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是矩形 |
 如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相平,则该几何体的左视图是( )
如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相平,则该几何体的左视图是( )


