题目内容
13.(1)计算:($\frac{1}{4}$)-1+|1-$\sqrt{3}$|-$\sqrt{27}$tan30°;(2)化简:$\frac{a}{{a}^{2}-1}$÷($\frac{a+1}{a-1}$-$\frac{1}{a-1}$).
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用绝对值的代数意义化简,最后一项利用二次根式性质及特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=4+$\sqrt{3}$-1-3$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=4+$\sqrt{3}$-1-3=$\sqrt{3}$;
(2)原式=$\frac{a}{(a+1)(a-1)}$÷$\frac{a+1-1}{a-1}$=$\frac{a}{(a+1)(a-1)}$•$\frac{a-1}{a}$=$\frac{1}{a+1}$.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
根据表中数据,估计在男性中,男性患色盲的概率为0.07(结果精确到0.01)
| 抽取的体检表数n | 50 | 100 | 200 | 400 | 500 | 800 | 1000 | 1200 | 1500 | 2000 |
| 色盲患者的频数m | 3 | 7 | 13 | 29 | 37 | 55 | 69 | 85 | 105 | 138 |
| 色盲患者的频率m/n | 0.060 | 0.070 | 0.065 | 0.073 | 0.074 | 0.069 | 0.069 | 0.071 | 0.070 | 0.069 |
2.与无理数$\sqrt{31}$最接近的整数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
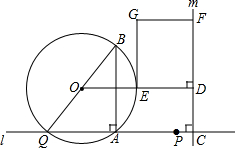 如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=$\frac{3}{2}$CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.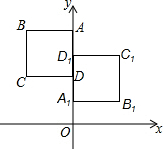 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).