题目内容
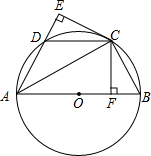 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且 |
| CB |
 |
| CD |
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
考点:全等三角形的判定与性质,勾股定理,圆心角、弧、弦的关系
专题:常规题型
分析:(1)可以证明Rt△CED≌Rt△CFB即可求得DE=BF;
(2)易证△CAE≌△CAF,根据直角三角形中30°角所对直角边是斜边的一半即可求得CF,BF的值,即可解题.
(2)易证△CAE≌△CAF,根据直角三角形中30°角所对直角边是斜边的一半即可求得CF,BF的值,即可解题.
解答:证明:(1)∵弧CB=弧CD
∴CB=CD,∠CAE=∠CAB
又∵CF⊥AB,CE⊥AD
∵在Rt△CED和Rt△CFB中,
,
∴Rt△CED≌Rt△CFB(HL)
∴DE=BF;
(2)∵△CAE和△CAF中,
,
∴△CAE≌△CAF(HL)
∴∠CAE=∠CAB,
∵AB是⊙O的直径
∴∠ACB=90°
∵∠DAB=60°
∴∠CAB=30°,AB=8
∴BC=4,
∵CF⊥AB
∴∠FCB=30°
∴CF=
,BF=2
∴S△ACD=S△ACE-S△CDE=S△ACF-S△CFB=4
.
∴CB=CD,∠CAE=∠CAB
又∵CF⊥AB,CE⊥AD
∵在Rt△CED和Rt△CFB中,
|
∴Rt△CED≌Rt△CFB(HL)
∴DE=BF;
(2)∵△CAE和△CAF中,
|
∴△CAE≌△CAF(HL)
∴∠CAE=∠CAB,
∵AB是⊙O的直径
∴∠ACB=90°
∵∠DAB=60°
∴∠CAB=30°,AB=8
∴BC=4,
∵CF⊥AB
∴∠FCB=30°
∴CF=
| 3 |
∴S△ACD=S△ACE-S△CDE=S△ACF-S△CFB=4
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证DE=BF是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知:当x=1时,代数式
ax3-3bx+4的值是7,那么,当x=-1时,这个代数式的值是( )
| 1 |
| 2 |
| A、7 | B、3 | C、1 | D、-7 |
用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是( )
| A、圆锥 | B、球体 |
| C、圆柱 | D、以上都有可能 |
已知扇形的圆心角为120°,半径为6cm,则扇形的面积为( )
| A、12cm2 |
| B、36cm2 |
| C、12πcm2 |
| D、36πcm2 |
 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )| A、1个 | B、2个 | C、3个 | D、4个 |
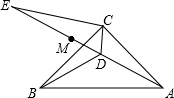 如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.